N+1.5.2 数学强加的题外话

.5.2　数学强加的题外话

没有不断的语言滥用就不会有任何发现、任何进步。

——费耶阿本德（Paul Feyerabend），

《反对方法》（Against Method）

现在，我们似乎已经陷入了僵局，我说的“僵局”的意思是：

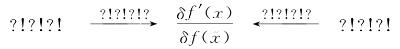
我们不知道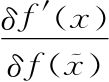）是什么。同以往一样，当我们的符号体操得出了我们不理解的表达式，可以回到稿纸上，问一下一切在最开始时的意义是什么。回想一下在求导数的时候，我们总是在找类似这样的东西：

也就是说，从吃某个（食物）的机器M开始。在这里，（食物）是整台机器f（x）。然后我们对（食物）做微小改变，从（食物）变成（食物）+d（食物），然后我们观察两种情形下机器反应的差别，即dM≡M［食物+d（食物）］-M［食物］，导数就是输出的变化dM除以输入的变化d（食物）。我们到底如何才能用这个思想求出下面这个

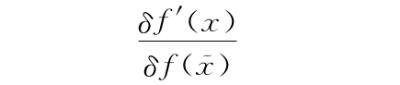
呢？嗯，根据一直以来的解读，下面的部分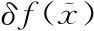，，就是（食物）的变化：δf是我们加到原来的函数f上的无穷小函数，目的是确定L［f（x）］的反应会如何变化。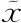让我们知道哪里改变了，f是我们在某点改变了值的函数的名称，δ只不过是告诉我们改变为无穷小的愚蠢标记。

这样我们就明确了改变的是什么：我们是对函数f做微小改变。这是说的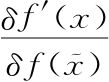的下面。那么上面部分呢，δf'（x）？嗯，再次用开始时同样的解读，这就是对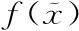做微小改变导致的f（x）的微小改变。关键是这个：我们改变了函数f（x）一点点，它的导数当然也就会改变一点点。但是，我们不是在对f（x）和f'（x）做两个独立的改变。f'（x）的任何变化都来自我们对f（x）所做的事情。由于δf'（x）只不过是“我们对f（x）做的微小改变导致的f'（x）的变化”的缩写，因此我们可以写成：

δf'（x）=（δf（x））'，

其中δf（x）是任意“微小的函数”。如果不明白，可以这样理解：奇怪的符号δf'（x）其实应当写作δ［f'（x）］以提醒我们它表示的是我们对f（x）做的改变导致的f'（x）的变化。因此，我们可以得到

δf'（x）≡δ［f'（x）］

≡［改变之后的导数］-［改变之前的导数］

≡［f（x）+δf（x）］'-［f（x）］'

=［f（x）］'+［δf（x）］'-［f（x）］'

=［δf（x）］'，

也就是说

δ［f'（x）］≡［δf（x）］'，

因此我们可以把撇号放到泛函导数的外面。我们做这些的目的是想知道如何处理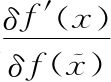），利用上面的等式可以得到

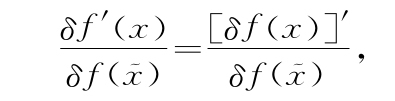
而这里的撇号指的是“相对于x的导数”，而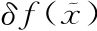相对于x不变，因为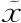指的是某个特定的格子，因此我们可以进一步得到

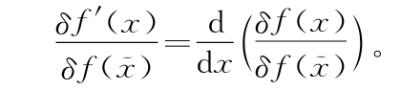
最后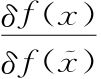，就是我们在前面介绍的“狄拉克δ函数”，这个函数处处为0，除了在处有一个无穷高的尖峰。因此我们就得到了非常离奇的等式

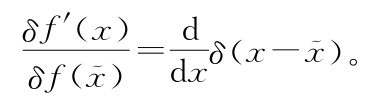
……现在怎么办呢？！