N+1.5.3 打破僵局

.5.3　打破僵局

严格只是没什么可做的了的另一种说法。

——来自珍妮丝·贾普林（Janis Joplin）的《我与布尔巴基·麦吉》（Me and Bourbaki McGee）[1]

在逐渐深入无穷荒野的过程中，突然冒出来了等式

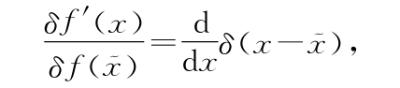
现在还完全不清楚这是什么意思。狄拉克δ函数的导数到底是什么？δ（x）函数本身定义为除了x=0之外处处为0。因此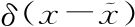项除了x=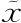之外处处为0。但δ（0）不是一个普通的数。在定义δ函数时，我们发现δ（0）可以视为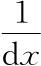，其中dx为无穷小，这使得δ（x）“干掉了积分”，即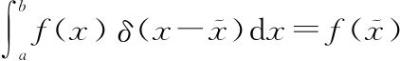，当然前提是位于a和b之间。这当然很好，但我们怎么确定一个无穷高无穷薄的尖峰的导数呢？！这个突然冒出来的表达式好像没什么意义。不过我们已经深入荒野，不能就此放弃。数学是我们的。我们自己创造的数学。因此让我们勇往向前，作出如下声明：

我们完全不知道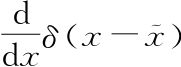是什么，因此就选择定义它为能遵循我们所知的关于导数的一切的任何东西，尤其是求导锤子和积分反锤子。

如果我们选择这样做，我们就不用知道δ（x）的导数是什么，但我们得知道它有什么性质：熟悉的情境！让我们来试试看能得到什么。这个令人困惑的探索始自我们被式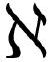（.19）难住时。我们被难住是因为我们不知道怎么处理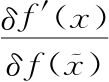。但是我们证明了无论它是什么，都可以视为δ（x）函数的导数，因此

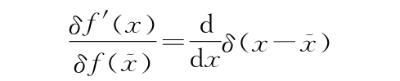
由此我们可以接着式（N.19）得到

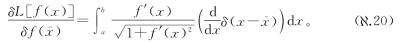
这个东西的右边看上去很复杂，但它具有形式

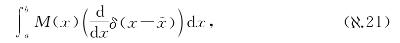
如果我们能处理这个有点吓人的一般形式，我们就能继续。怎么做呢？好吧，就由我们来决定！我们定义δ函数的导数为遵循锤子和反锤子的某种东西，因此根据定义我们可以应用这些。说具体点，如果我们能将式（.21）中的求导从δ移到M前面就好了，因为我们知道怎么处理δ函数，它会干掉包含它的积分。我们想移动求导，幸运地是我们有做这个的工具：第6章的相乘反锤子。将其应用于式（.21）得到下面这一大堆好玩的东西：

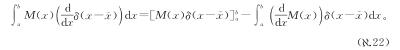
右边的第一项就是0，除非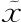=a或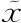=b，因此我们假设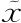不是端点a或b中的一个，这样我们就可以继续。拿掉那一项之后，我们得到

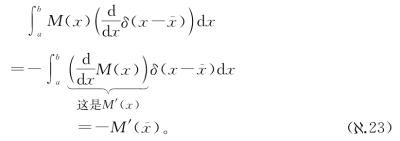
漂亮！这样我们就知道了δ函数的导数对积分内部的任意函数起什么作用，

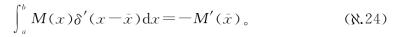
注意这个与原来的δ函数本身的定义的性质有多相似，也是以稍微不同的方式干掉积分：

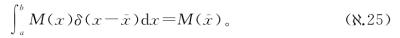
发现了δ函数出现在积分内部时的作用后，我们可以回到式（.20）继续。可以得到：

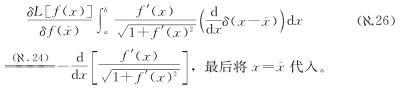
幸运地是，根据我们最初的目标，我们不用实际计算这个可怕的导数。我们想知道的是将弧长泛函的导数设为0（从而求出哪些函数是函数空间中的“平点”）是否能得出我们从直观上已经知道的结果：即两点间的最短路径是直线。为此，我们将上面的整个式子设为0，这样我们实际得到的是

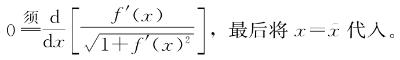
因此我们要求上面的等式对所有可能点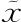都成立。但上面的等式就是某个东西的导数，而如果某个东西的导数在所有点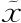都为0，那这个东西肯定是常数。因此，我们得到

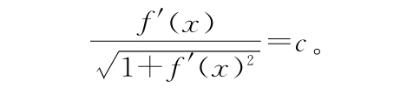
现在不知道该怎么做了，不过也许我们可以做一些符号体操，我们可以提取出f'（x）。对上面的等式两边取平方，将分母移到右边得到

［f'（x）］2=c2（1+［f'（x）］2=c2+c2［f'（x）］2。

这告诉我们

［f'（x）］2（1-c2）=c2，

因此，

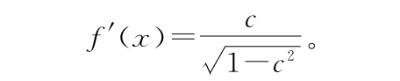
而如果c只是一个我们不知道的数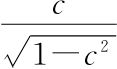，也是一个我们不知道的数，因此我们可以重新缩写，将整个东西称为a。这样就得到

f'（x）=a。

啊哈！f的导数是常数！这表明f是直线。也就是说（我们现在可以说一些真正神奇的东西了），在我们的无穷维函数空间中使得弧长泛函最小的点就是直线。为了庆祝，我们将这个尽量写得专业一点，配得上我们现在的兴奋之情：

！！！是！的！！！　　f（x）=ax+b　　！！！是！的！！！

提醒一下自己为什么我们这么关心这个，这个结果之所以让人兴奋不是因为我们推导出了两点之间的最短距离是直线。这个我们无需数学就能知道。这个结果让人兴奋是因为它让我们更加自信我们在这一章发明的同类相食微积分处在正确的轨道上，而且，它确实有用。只需一些简单的运算，除了少许标记变化，与单变量微积分的运算基本一致，我们就能有效地在整个无穷维的函数空间搜索某些具有特定性质的函数，在这个例子中的性质是最小化弧长泛函。

在某种意义上，我们符号化地“考虑”了两点之间可能路径组成的大得难以想象的空间，并找到了两点之间的最短路径。这个结果是我们自己发明数学之旅的一个非常重要的里程碑。它标志着我们获得了一个新的超能力：对无穷维空间进行有效推理的能力。利用这一章的方法，只需一个泛函，我们就有可能找到使得它最大或最小的函数。

我们的旅程已经走了很远。我们从加和乘攀登到了无穷维微积分，我想是时候告一段落了。让我们总结一下这一章做的事情，再在下一插曲放松一下。我们该去哪儿？海滩？我们可以称之为“插曲：堆沙子城堡”之类的。或者我们可以回到书的前面，将一堆句子的顺序打乱，迷惑在读那些章节的过去的我们，再看看现在我们还会不会迷惑。如果你读了哪条语句后感到迷惑……也许这就是原因。说真的，你想去哪儿？我还从没让你决定过插曲去哪儿？你不用马上做决定。还有整合没写。但无论做什么，请放松自己，并且最重要地是，一定要远离学校。我们有资格这么干。

[1] 好吧，并没有这首歌。不过应当尽可能提供引用出处，因此如果你在寻找上面这句并不存在的歌词的出处，请引用第一手来源：这本书的第366页。