N+1.5 无穷奖池：让我们的思想为我们服务

.5　无穷奖池：让我们的思想为我们服务 .5.1　通过重新发明已知来检验我们的发明

面对美的这种颤栗感，在数学之美的驱使下进行探索，并在自然中找到确切的应证，这种不可思议的事实说服了我，认为美才是人类心智最深刻的关切。

——钱德拉塞卡（Subrahmanyan Chandrasekhar），《真理与美》

（Truth and Beauty：Aesthetics and Motiuations in Science）

对单变量、多变量微积分与同类相食微积分的相似性谈论了这么多，还是有一个问题没有回答。我们选择的定义使得同类相食微积分的导数计算仍然与以前类似。我们迫使同类相食微积分的导数的性质与单变量和多变量微积分足够类似，这样我们在计算导数的时候就不用学习任何新的东西。我们只是将标记从∂和d改成了δ，我们还写出了这类看似很高深的等式，而这其实就是对等式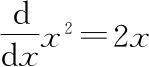的推广和伪装。

但是，到目前为止还是不清楚具有这种性质的简单定义导数能不能保留其他性质。我们能在多大程度上认真看待新思想和旧思想之间的这种相似性？例如，

在单变量和多变量微积分中，我们可以通过求出机器导数为零的点来寻找机器的平点[1]。但是现在我们所有的等式都在两种不同的解读之间摇摆不定：一种将机器视为可以在二维中绘制的熟悉的曲线。另一种将机器视为“有无穷多个格子的向量”。因此，如果我们从一个同类相食机器开始，比如

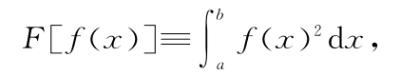
然后对“向量”f（x）的所有格子令其泛函导数为0（即，对所有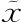），这时也还是完全不清楚这个过程最后的结果是不是在某种意义上使得泛函取最大或最小的位置。用我们一直以来使用的技术计算泛函导数并不必然就意味着“导数等于0”仍然是“平点”。

基于一贯的做法，我们不会去翻阅课本看“导数等于0”是不是仍然意味着“平点”。我也不能直接说“是的，就是这样。让我们接受这个事实。”因此，如果我们想搞清楚是否在某种有用的意义上“导数等于0”仍然意味着“平点”，我们就应当采取一直以来的做法：检验一些简单的情形，看我们的新思想能否给出期望的结果。

首先，让我们看一下上面这台熟悉的同类相食机器，即

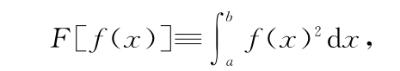
由于f（x）2从不为负，因此很显然没有哪台机器f能使得F［f（x）］为负。而且，唯一能使F［f（x）］等于0的机器f是f（x）≡0。从图形的角度来思考这个积分，如果f（x）存在非零值，无论正负，则在一段小区间内所有点都有f（x）2为正，因此面积就会大于0，从而使得F［f（x）］大于0。因此从直观上可以看出，在由所有机器组成的空间中（管他什么意思）机器f（x）≡0会使得F［f（x）］取最小值。因此，在我们新的同类相食微积分中，如果“导数等于0”仍然意味着“平点”，对于这种情形如果我们还做原来的优化，数学给出来的答案就应当是f（x）≡0。[2]我们来试一下。如我们所知，F的泛函导数是

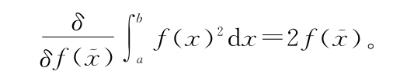
令下面的式子对所有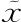格子成立

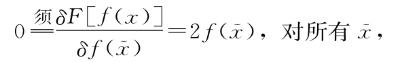
这其实说的就是对所有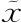有，f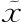（）=0。因此f始终为0，与我们事先预计的相符。很好！我们再用一个简单的例子检验一下新思想的有效性。在第6章末尾，我们证明了机器图形的弧长——即在a和b之间的长度——可以写为

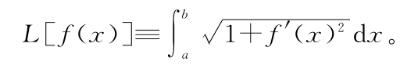
我们通过放大机器的图形，应用捷径公式，然后又缩回来，将微小长度相加证明了这一点。

我们从直观上就能知道两点之间的最小距离是直线，用我们的高能新机器来证明这一点没什么意义。不过我们可以用这个来检验同类相食微积分技术的有效性。背后的理由与前面是一样的：如果我们的同类相食微积分技术的确能如我们所预期的那样，那么对于这种情形，“导数等于0”方法给出的使L［f（x）］取最小值的答案就应当是直线。如果答案不是这样，我们就知道这个定义的性质并不符合我们的要求。

另一方面，如果这个过程的确给出了语句“f是直线”，就能让我们更加确信同类相食微积分处于正确的轨道上，而且对于我们事先不知道答案的情形可能也会继续有效。我们来试一下。取上面定义的L［f（x）］的泛函导数，如下：

然后怎么办？

[1] 即课本上的行话说的局部极大值、局部极小值、鞍点。

[2] “优化”一词指的是我们熟悉的寻找平点的过程，即令导数等于0，然后求出能使得条件成立的点。