N+1.4.2 古怪的语法习惯

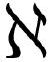虽然有式（.9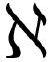）—（.11）之间的相似性，大部分变分法的教材在计算泛函导数时采用的却是相当不同的舞步。即便应用数学和理论物理的课本也是如此，在这里严格性的标准应当和纯数学很不一样，使得这种奇怪的舞步显得很不合适。请尝试多看一会后面的例子，但如果觉得迷惑也不要担心。它们的舞步是这样的：考虑如下形式的积分泛函

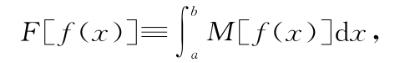
然后它们定义

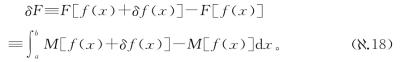
到这里他们通常会说，“用δf（x）的幂展开M［f（x）+δf（x）］”，得到类似这样的东西

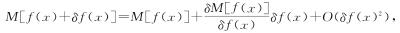
其中O（δf（x）2）表示“取决于δf（x）的2次或更高次幂的东西”。然后他们将上面的展开代入式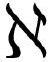（.18），并忽略O（δf（x）2）中隐藏的所谓“高阶项”得到

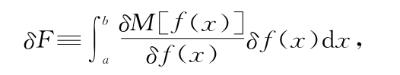
而泛函导数则定义为积分内部的量，即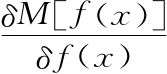。注意这个答案与我们前面得到的完全一致，但上面的讨论有几个地方与我们熟悉的单变量和多变量微积分很不一样。首先，我们假想的这个虚拟课本用了某种类似怀旧装置的东西来展开M［f（x）+δf（x）］项。这使得展开的M［f（x）］项与-M［f（x）］项抵消了。然后高阶项被神秘地去掉了。这么做的理由是如果我们将δf（x）视为无穷小函数，类似于单变量微积分的dx，则（δf（x））2就应当无穷小于δf（x），因此有理由忽略它，以及所有高于2次幂的项。另外，注意到定义泛函导数的这个讨论开始时并不是寻找什么可以被合理称为泛函F的导数的东西，而是寻找导数的上半部分，这就是说，只是寻找δF项。然后在计算δF的过程中刚好出现在积分内部的某个东西被直接定义为泛函导数，却没有给出任何这样做的理由，或者积分内部的这个神秘项为什么值得被称为导数。这个古怪的论证的确得出了与我们前面的讨论相同的答案，但是相当绕圈子和让人迷惑。

就我自己的经验来说，我从外围观察了变分法很久，每当在课本或黑板上看到它的时候，心里就想，“喔！真复杂，”而其实每个理解基本微积分的人已经掌握了90%理解变分法所需的东西。只不过是（1）标记的不同，和（2）课本上通常用来计算泛函导数的不同舞步使得它看起来像是截然不同的领域，来自非常陌生的思想。

当然，上面这些思想在课本中有多种等价的形式化，但就像我们之前多次讨论的，逻辑等价远远不意味着心理等同。甚至在正式讲授之前，只需反复强调所有这些吓人的“新”东西与学生已经熟悉的“旧”东西有多相似，就可以消除许多困惑。至少我一直以来的感觉是这样。如果你厌倦了听我一次又一次说同样的东西……很好！现在尝试回忆一下在读其他课本时的反复抱怨，这些也许就会更有意义一点。