N+1.4 无穷维微积分的教学缺陷

.4　无穷维微积分的教学缺陷 .4.1　对积分泛函的难解偏好

在这门课的传统讲法中，并不经常澄清同类相食微积分与多变量微积分的相似之处，更不要说单变量微积分。例如，在变分法中，计算泛函导数的具体例子通常关注于所谓的“积分泛函”——即类似这样的同类相食机器：

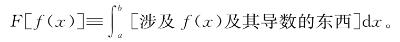
我们已经见过的一些“积分泛函”的例子，包括积分本身，

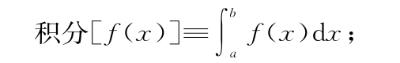
弧长泛函，即f的图形的长度，

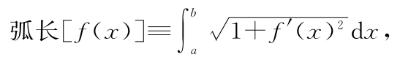
以及“范数”，即将f解读为无穷维空间的向量的长度。前面说过这个“长度”与前面的弧长没有关联，是将向量“长度”的概念推广到无穷维。这会得到：

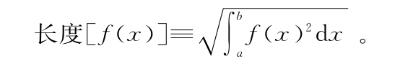
课本上通常将这个写为‖f（x）‖或‖f‖而不是长度［f（x）］，但意思是一样的。现在，基于这个背景，（我打赌）大部分人在第一次接触这门课时都会有一个问题，但我从没见过有哪本书解释过：为什么同类相食微积分几乎无一例外都关注“积分泛函”，而不是不一定要写成积分形式的更广义的泛函？学生有疑惑是对的，因为原因其实相当微妙。

的确，来自实际问题的泛函例子大部分　是积分泛函，但是同类相食微积分教学之所以不愿意用更广义的例子来向初学者展示同类相食微积分与多变量微积分的相似性是出于其他原因。首先，注意在所有积分泛函中，无论何种形式，f（x）中的x都表现为“约束变量”。用几个例子解释一下是什么意思，以及为什么这个有影响。考虑积分泛函

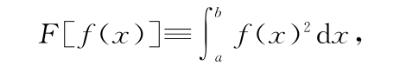
根据我们的词典和前面的讨论，它在多变量微积分中对应于

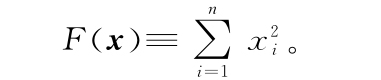
我们已经看到，通过适当选取泛函导数的定义，我们能将多变量微积分中的表达式推广为同类相食微积分中的类似表达式，在这个例子中是将

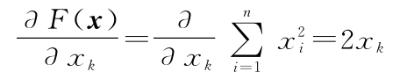
推广为

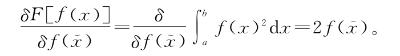
在课本中，很少用简单具体的例子来澄清这两种计算之间的直接关联，但这不是这里的重点。重点是：为什么经常是积分泛函？为什么这门课的教材在举例时很少给出形为

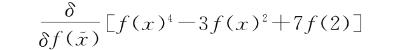
这种涉及泛函导数而不是积分的表达式？就算这样的例子在应用中不重要，它们对于教学却相当重要，因此值得问一问为什么它们在变分法教科书中如此稀少。利用我们的词典，可以发现与上面这个多变量微积分的表达式对应的是

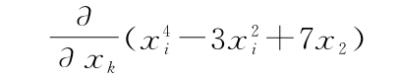
索引i是“自由的”，或未定的，不是出现在（比如）求和中，那样将所有可能值加起来时它的具体值是无关紧要的。由于i是未定的，对前面的偏导数的计算就必须考虑两种可能：要么i等于k，要么不等于。利用上一节介绍的“克罗内克δ函数”的标记，我们可以同时符号性地考虑两种可能，写为

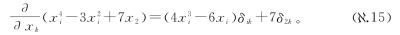
式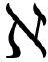（.15）这样的表达式在多变量微积分的引论部分经常出现。但是将上面例子转换为同类相食微积分语言的类似表达式却基本不会出现在标准教科书中。转换后我们得到

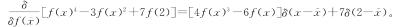
虽然让x保持未定在这里似乎没什么意义，但却很难不注意到上面的例子中变分法与单变量和多变量微积分中做法的直接类比。然而，像这样具有重要教学价值的“没用”例子在这门课的标准教法中很少展现。那为什么这样的例子在数学课本中很少展现呢？我想至少有如下一个原因。如果我们计算f（x）3相对于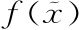之类的泛函导数，会得到启发性的表达式3f（x）2δ（x-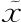），则要么x不同于x，这时整个表达式为0，要么x=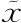，这时表达式等于

3f（x）2δ（0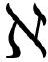）　（.16）

我相信，这就是数学课本中通常不给出这样简单的例子的原因。多变量微积分的对应例子会给我们一个干净的有限大小的表达式，而变分法的例子中则附带有“无穷小”的数δ（0），而根据许多数学课本的传统，这不被认为是一个有意义的表达式。而如果目标是给出这些概念在实数系中最优雅的“严格”形式化，将狄拉克δ函数禁锢在积分中的做法如此普遍就不难理解了，但这样却不利于对同类相食微积分的概念理解。根据我自己的经验，物理专业研究生对变分法的具体计算的熟悉程度远不如大部分数学专业的研究生。这是可以理解的，大部分数学家不想让涉及狄拉克δ函数的表达式出现在积分外面，而涉及“积分泛函”的类似表达式则被认为是洁净的。要明白为什么，想一下我们可以将δ（0）视为1／dx。因此，只要将上面的表达式都放到积分中，所有“无穷小”就都消失了。将上面的式子放到积分中（并假定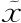位于a和b之间），我们得到

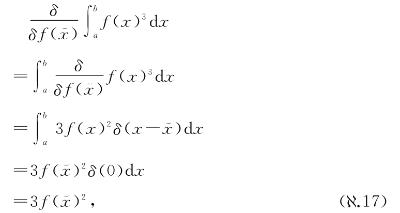
最后的两步彻底犯了忌。不过，就当删掉论证中涉及δ（0）的那一行，直接给出最后的结果。如果这样做，与原来的计算相比，或者与式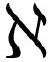（.16）相比，多数数学家会觉得这样更舒服，式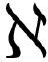（.16）涉及δ（0）是因为在没有积分保护的情况下取了泛函导数。我认为，这就是你通常会看到变分法教材和课程如此关注“积分泛函”的原因。只要我们限于积分泛函，所有泛函导数给出的表达式就可以避免思考δ（0）之类的东西。我必须强调的是数学家们在课程和教材中呈现同类相食微积分的方式在逻辑上没有任何不对的地方。但是，由于牺牲掉了上面这种简单例子所能给予的“啊哈！”领悟时刻，我认为这种标准呈现方式在教学上是极不正确的。

说了这么多之后，我应当花点时间替标准教材辩护一下。在许多方面，我们假想的数学家的偏好都很有意义。δ（0）这样的东西在实数系中很难定义，因此在将这一章的思想形式化时面临一个真正艰难的选择：

1.坚持实数系，在将δ函数（和相关的对象）形式化时，不说δ（0）之类的，而代之以“测度”“分布”或“检验函数空间的线性泛函”之类的说法。

2.离开舒适的实数系，进入超实数系之类的东西，在其中无穷大和无穷小量被严肃对待。

如果目标是为这一章的概念发展出具有主流数学文化认可的严格性的形式理论，第一种选择就是更好的选择。那么我在这一章所批评的做法就不应当受到责难。如果我们的目标都是这个，标准做法就是达到这个目标的完美做法。

好了，在上面的讨论中，我们遇到了到这本书中一贯以来核心的前数学主题：更关注创造数学概念的思维过程，而不是这些数学概念可能衍生的大量推论。每个数学概念都存在不同的可能定义，泛函导数也不例外。虽然任何讨论最终都必须选择其中一个定义才能往下推导定理和构造证明，但只有探讨过不同候选定义的相对优缺点之后，我们最终才能透过打磨过的数学概念的形式化，理解最初推动这些发现的非正式的不受拘束的推理。