N+1.3.4 在d→∂→δ的变化中再增加两个δ

.3.4　在d→∂→δ的变化中再增加两个δ

这样我们就找到了能得出有限大小答案的泛函导数定义。考虑过各种可能的定义的推论后，我们对单变量、多变量和无穷维微积分之间的关系以及为什么后者是这样有了更清晰的认识。例如，如果我们选择式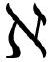（.8）的定义，就不难看出下面等式之间的相似性，虽然标记从d变成了∂又变成了δ，从什么都没有变成了∑又变成了∫：

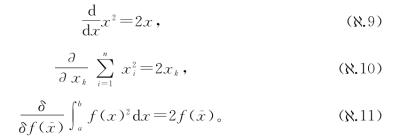
如果我们不对所有变量求和，只是对某个特定的平方项求导，同样的相似性依然成立。很快我们就会看到这一点，但我们需要先讨论一下传统标记的两个互锁项。之前，我们曾将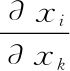定义为在下标相同时为1，不同时为0。课本上称这个为“克罗内克δ函数”，听起来很炫，记为

虽然“克罗内克”这个名字可能让人联想到某个关押最危险罪犯的小岛监狱，它的思想其实却很简单。注意让人混淆的标记神奇地相遇了，符号δij与无穷维微积分中替代d和∂的δ没有关联。

我们还将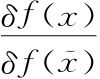）定义为x和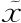相等时为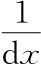，不等时为0。你不会觉得奇怪，课本上为这个也取了好笑的名字。课本上称这个为“狄拉克δ函数”，这个术语不怎么好，不过我们还是会容忍它，因为它是以一个极为古怪而杰出的家伙的名字命名的。虽然课本上通常不这样写，狄拉克δ函数还是可以定义为：

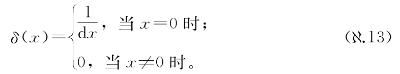
我们可以将这个函数视为几乎处处为零，除了x=0之外，在这一点可以将其视为“无穷高的尖峰”。我们可以将上面的定义表示为稍微复杂一点但与克罗内克δ函数的类比更清晰的形式：

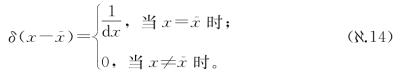
现在可以看出来这个与克罗内克δ函数完全类似，在其中：（1）两者的δ符号的描述都有两个“变量”，（2）当这两个变量不相等时，两个δ符号都等于0，（3）当两个变量相等时，δ符号的取值将使得多变量微积分与变分法有相同的性质。最后这句话可能不是很清楚，我们用一个例子来说明一下。

在式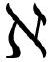（.9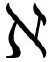）、（.10）和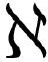（.11）中，我们展示了3种微积分的相似性：单变量、多变量和同类相食（你愿意的话也可以称之为“变分”或“泛函”之类的）。利用这些新的δ符号，我们可以用另一种方式展现这种相似性，而不用对所有项求和。论证过程与我们在第3章发明重新缩写锤子（“链式法则”）几乎是一样的，我们得到

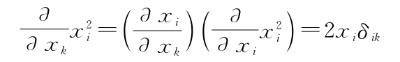
和

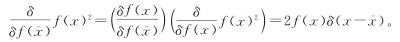
因此，用这两个新版的δ符号（克罗内克和狄拉克，在上面两个等式的右边，与左边泛函导数的δ符号没有关联……明白了为什么我抱怨标准标记吗？搞得我写出这样的句子！），我们可以用另一种方式揭示这3种微积分的相似性：

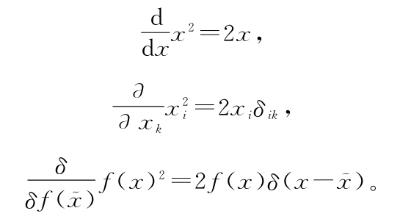
看明白是怎样相似的吗？当然，出于各种历史和文化的复杂原因，数学家（以及他们写的数学书）通常都不会这样讲授变分法。下一节我们会简要说一下这门课的形式化以及讲授方式中一些更令人讨厌的方面。