N+1.3.2 无穷前数学，第1部分：他们从未讨论过的一种可能

.3.2　无穷前数学，第1部分：他们从未讨论过的一种可能

到这里好像进行不下去了，因为我们不清楚符号

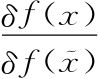
指的是什么。不过这个东西是我们自己发明的，因此与其问“下一步该怎么办？”不如问一下，“我们想要F［f（x）］的导数是什么？”如果觉得这像是反向推理，再想一下！请记住在这本书中我们是在做什么。将以前熟悉的概念推广到狂野奇异的领域时，总是需要进行选择。要选择的是：用原来的概念的哪些方面来建构更一般的新概念？这里，我们很快会看到，要选择的其实是我们想让导数

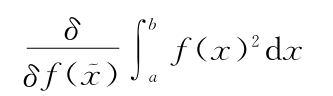
等于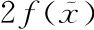）还是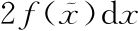dx。接下来我们就会看到为什么。回到前面的计算，我们停下来是因为我们还没有明确

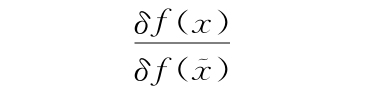
是什么意义。如果我们不说清楚想怎样定义不同的“向量格子”f（x）和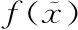相对于对方的泛函导数，就无法进一步定义同类相食机器F［f（x）］的泛函导数。也许我们的词典能帮上忙。回想一下在单变量微积分中，我们有

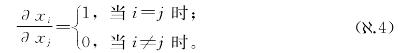
这其实说的是不同变量x1，x2，…，xn可以视为“相互垂直的方向”，因此沿着其中一个前进的时候不会改变在其他方向上的位置，就好比朝东或朝西走不会改变沿南北轴的位置一样。由于我们可以按自己的意愿进行推广，因此可以选择定义

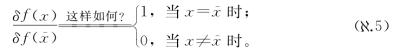
如果这样选择，我们就能继续推进，前面的泛函导数就会变成

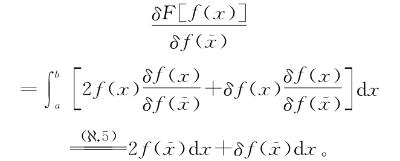
注意每一项都包含dx，因此每一项都是无穷小。但是，第二项是两个无穷小相乘，所以要无穷小于第一项。因此，有了这个定义，我们可以说

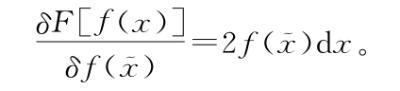
这个说的是式（.5）作出的选择使得所有泛函导数都是无穷小。从直观上来说，为什么是这样呢？在多变量微积分中，式（N.4）作出的选择，即

使得偏导数一般为普通的数，不会是无穷小或无穷大的数。例如，在多变量微积分中，

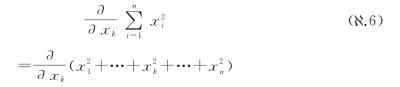
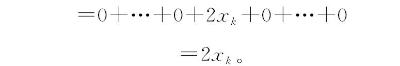
注意取导数后并没有dx之类的无穷小量附在后面。为什么这里在做出式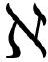（.5）的选择后，我们会得到如下结果呢？

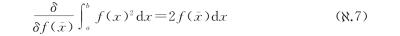
这两个式子是如此类似，以至于很难明白为什么会一个得出正常的数另一个得出无穷小。其实，我们可以再次无视标准教科书的谨慎，直接得出答案。式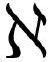（.6）的求和是对有限大小事物的求和，因此毫不奇怪我们得到有限大小的导数。而式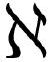（.7）的积分是对无穷小事物的求和，它是无穷薄的矩形面积的求和，其中每一个都类似f（某个数）dx，而f（某个数）是3或7或52这样的普通数，dx则是“无穷小”量。因此，像式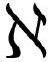（.5）那样定义“偏泛函导数”——这样做是因为我们想尽量像式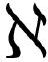（.4）那样定义它们——最终导致了我们的泛函导数成为无穷小量。

直观上来说这是对的。如果我们将机器图形在某一点的高度改变无穷小量，机器图形下的面积会改变多少呢？答案肯定会附有两个无穷小量：原矩形的无穷小宽度（来自dx）和高度的无穷小变化（来自δf（x））。因此，如果我们选择像式（.5）那样定义“偏泛函导数”，整个面积的变化率附有一个无穷小量就说得通了，因为计算导数时除以δf（x）会抵消两个无穷小中的一个。