N+1.3 发明同类相食微积分

.3　发明同类相食微积分 .3.1　同以往一样，循旧立新

我们最关注的不是对象的本质，而是它们的性质。这是数学中永恒的真理，我们从一开始就认识了这条原则。的确有许多可能的面积或斜率定义，与我们采用的定义性质不一样。那些定义可能比我们的定义要复杂得多，研究起来也困难得多。但是，我们的定义的性质符合我们的需要，因为我们要求它们这样，也因此我们可以只关注它们。虚空中有无穷多种机器，其中大多数都比我们在第5章研究的4种类型的机器复杂得多，但我们选择研究这4类特殊的机器是因为我们确切知道关于它们可以说些什么。我们也知道我们关于它们的说法是准确无疑的，因为我们就是根据它们的性质来定义它们的。

这里我们面对的是同样的原则，只不过有了不同的伪装。抛开教科书的条条框框，我们应该怎样定义吃进去整台机器吐出来数的机器的导数，才能对它们执行我们原先可以执行的相同操作呢？课本上的习惯做法是先定义一些要谈论的函数（就好像那是驱动数学创造的首要关切），然后再往下推演结果。我们不想忍耐这种做法，宁愿采取相反的途径。我们将采用前数学的方式来推导无穷维微积分的定义，保持我们所谈论的函数的具体位置为未知，迫使这些新的对象——不管它们可能是什么——性质像我们熟悉的微积分一样符合我们的要求，然后再向前推进。最重要的也许是，在这个新的世界里“导数”的意义到底是什么，我们应当要求导数还是可以视为一个无穷小量除以另一个无穷小量。只有这样才能将到目前为止我们在这本书中发展的微积分知识带进这个野性的荒野。至于到底是什么对象遵循这样的操作，以及如何用集合论的语言描述这些对象，那都是以后的事情，可以留给对这些工作感兴趣的人完成。一旦尘埃落定，如果最后发现研究的对象与最初预想的不一样，那也只能接受。我们不关心本质。

因此，假设我们得到了一台同类相食机器，意思是吃进去整台机器f（x）吐出来一个数F［f（x）］的机器。在多变量微积分中我们定义了偏导数：从机器F（x）开始，对x的一个格子做无穷小变化，其他格子保持不变，然后观察变化之前和之后输出的差异，并除以输入在之前和之后的差异。本着循旧立新的精神，我们可以用一模一样的方式定义无穷荒野的导数。

给定同类相食机器F，我们有无穷多个可以变化的“格子”。对吃向量的机器，这些格子标记为x1，x2，…，xn。现在，对吃整台机器的机器，这些格子标记为f（0），f（0.001），f（3），f（796.5），等等。我们无法具体列出每个格子，但每个数x都对应一个。对于向量x，x3标记位于第三个格子的数，现在符号f（x）标记的则是位于机器f的第x个格子的数。据此，我们开始定义同类相食机器的“偏导数”。

首先缩写：

δF［f（x）］≡F［f（x）+δf（x）］-F［f（x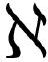）］。　（.3）

在解释其意义之前，有必要强调的是，不用d而用怪异的符号δ不是为了迷惑你，而是为了让你能看出标准教科书上喜欢用的符号所表达的思想其实是多么简单，与单变量微积分是多么相似。如果δ吓到了你，本着对数学的爱，请把我写的符号划掉，重新写成d。无论用哪种符号，这些等式表达的都是相同的内容。

好了。在上面的等式中，符号δf（x）表示一台无穷小机器，就好像dx在单变量微积分中表示一个无穷小的数一样。之所以说这台机器是“无穷小”，依据的是我们在式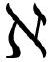（.2）中对机器“长度”或“大小”的定义，这个定义是受捷径公式启发。如果根据这个定义机器的长度为无穷小量，就说它是“无穷小机器”。关键在于，同单变量微积分一样，δf（x）中的f与f（x）中的f不是一回事。[1]

对于标记还有一点：F［f（x）］写成F［f］可能更正确，因为它不是依赖于某个具体的x值，而是整台机器f。不过，根据我的经验，从长远来看用F［f（x）］更不容易混淆。因此，当我们需要说明相对于哪个具体的格子求导时，除了x我们还需要另一个字母。我们不会用y之类的，这容易让人联想到“垂直”，而是用x。x上面的波浪线是说“这是一个不同于x的符号，它们指的可能是也可能不是相同的点”。仅此而已。好了，有了这些之后，根据我们的词典，我们可以定义F相对于特定格子f（x）的导数为

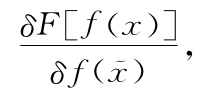
其中δF［f（x）］的定义同等式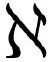（.3）中一样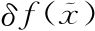，就是某台不相关的无穷小机器δf（我们让它的具体形式保持未知，就像我们最初对变量的处理一样）在喂进去输入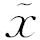时的输出。我们用实际例子来说明一下。假设我们有一台特定的同类相食机器

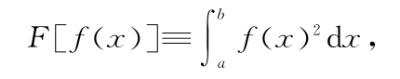
则根据前面的定义，

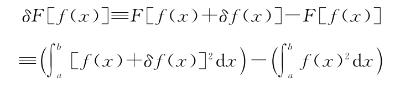
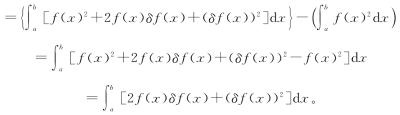
因此直接除以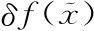），得到

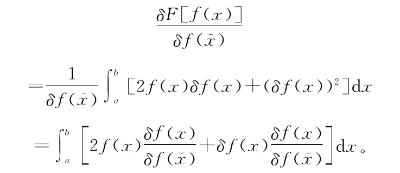
[1] 这一点需要解释一下：在单变量微积分中，标记x+dx指的是x加上一个无关的无穷小量。写“x+dx”时我们写了四个符号：（1）x，（2）+，（3）d，（4）x。我们知道第（1）个x与组成第二项“dx”的第（4）个x毫无关联。单变量微积分中的标记dx不是对数x做某种操作得到的东西；它就是一个（不相关的）无穷小量。虽然我们已经知道这个，在理解等式（N.3）中的缩写时还是有必要强调这一点。然而，令人迷惑的是，在许多数学领域中，d（某物）中的d确实指的是作用于跟在后面的（某物）的操作，而且变分法课本中也经常这样使用δ，以表示他们所说的“变分”。现在先不用担心这个。后面我们还会遇到这个思想。