N+1.2.3 在无穷荒野中度量长度

在插曲1中，我们发明了捷径公式，也就是勾股定理。首先，注意我们可以将这个公式解读为关于二维向量的事实。向量v≡（x，y）的x和y成分就是长度，并且它们相互垂直，所以向量的长度是

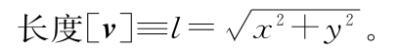
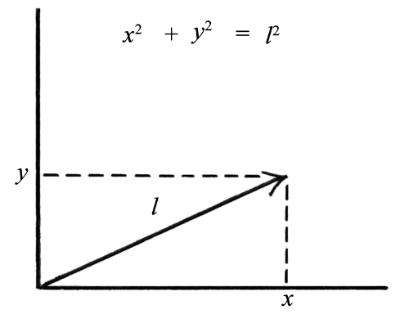
图.1　捷径公式告诉我们向量v≡（x，y）的长度为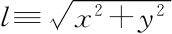。这将启发我们定义无穷荒野中的长度。

现在的问题是三维、四维是不是也有类似的公式。由于二维向量的长度公式中有很多2（即每个成分都取2次幂之后求和，然后整个取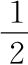次幂），我们可能会认为这个与向量所处的维度（2）有关，整个公式的指数（也与2有关）不是出于巧合。因此我们可能会猜测三维向量v≡（x，y，z）的长度公式是

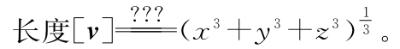
我们确实可以选择这种度量，[1]但如果我们想让这个度量与我们的日常语言相符，就不能这样选择。虽然我们可以这样做，可以发明任何我们想要的东西，长度却有每个人无需数学就能懂的独立的日常意义，因此如果我们想让“长度”的意义符合日常观念，三维或四维或n维向量的长度就不是我们可以任性发明的东西，而是我们必须去发现的东西。因为目前我们仅有的用来解决这个问题的原材料就是二维的捷径公式，因此有必要问一下我们能不能用这个公式去发现相应的更高维的未知公式，并最终将其扩展到新的无穷维荒野。

如图.2所示，的确有可能根据二维版本的捷径公式建立三维的捷径公式。这个论证表明三维向量v≡（x，y，z）的长度是

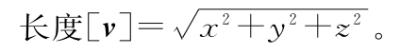
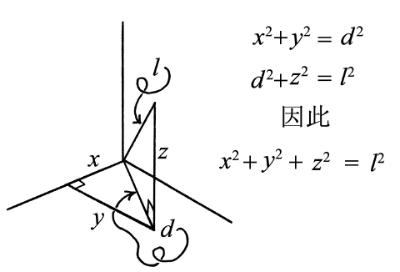
图.2　两次应用捷径公式就能建立原公式的三维版本。这幅图表明三维向量v≡（x，y，z）的长度是。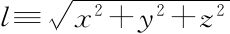

现在，反复应用二维版，我们就能建立类似的n维捷径公式。显然它有相同的形式：n维向量x≡（x1，x2，…，xn）的长度是

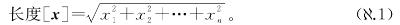
现在如果我们认真对待机器和向量的类比，就应当能定义机器的“长度”或“大小”，只需将机器解读为具有无穷多格子的向量就行了。这样我们就可以得到无穷维空间的某种“捷径公式”，在这个意义上，它将是一个关于无穷维几何的陈述。这听起来好像挺复杂，但其表面上的复杂主要是我们用来描述这个思想的词汇的错，比如“无穷维空间”之类的。虽然语言看似复杂，背后的思想却极为简单。我们只需照着词典推广公式（.1）就可以了。也就是说：如果我们将机器视为向量，则式（.1）告诉我们的是，机器的“长度”应当这样计算：（1）取每一格的平方，（2）都加到一起，（3）在整个式子上面放一个平方根符号。即：

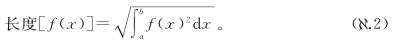
依葫芦画瓢推广捷径公式后，我们就可以谈论所有那些让自己显得很聪明的东西了，比如“将函数f视为无穷维空间中的向量时，长度就是积分f（x）2的平方根”。而且我们也确切知道这种形式的语句是什么意思，虽然我们压根画不出自己所说的东西！投机取巧，对吗？我们怎么知道这是对的？嗯，同以往一样，如果我们想让无穷维空间的性质类似我们熟悉的有穷维空间，就只能将无穷荒野的长度定义为式（.2）。到目前为止我们从事的还不是标准数学而是前数学，因此前面的论证不存在对和错。这只是用数学概念基于一个显然的理由论证了我们在一开始对无穷维长度的具体定义的选择。

现在我们定义了机器的“长度”的概念，我们可以谈论比如“什么什么机器是无穷小”。也就是说，现在我们可以在无穷荒野中谈论大小了，我们可以探索一下如何发明无穷维微积分的思想了！

[1] 数学家也的确这样做了。这种度量长度的方式称为“三阶范数”。将其作为长度定义是完全合理的，不过它与三维空间没有特别的关联，它与我们日常的长度意义也不相符，因此在这里我们不关注它。