N+1.2.2 数学中的同类相食

通过严肃对待机器和向量的类比，我们建立了上面的词典，这样我们就可以将关于向量的陈述转换为关于机器的陈述。但是在建立词典时我们写下了一对不是很熟悉的符号，比如F［f（x）］。[1]我们应该先问清楚我们研究的是什么对象。多数多变量微积分研究的是吞进去一个向量x吐出来一个数F（x）的机器。因此，认真对待向量／机器的类比意味着在变分法中，我们研究的是吞进去整台机器f（x）吐出来一个数F［f（x）］的机器。这种吞食同类的机器通常称为“泛函”，其实我们已经见过几种泛函，虽然我们当时没有这样看待它们。例如，

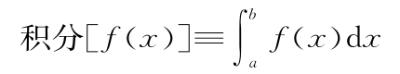
本身就可以视为一台机器，即吞进去整台机器f（x）吐出来一个数——x=a和x=b之间f（x）的图形下的面积——的“大机器”。将不同的机器喂给同类相食机器“积分”会得到不同的数。

另一个我们已经遇到过的例子是所谓的“弧长泛函”。在第6章末尾，我们证明了积分

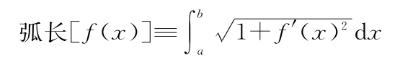
可以视为一台吞食整台机器f（x）吐出来一个数——x=a和x=b之间f（x）的图形的长度——的大机器。

还有一个泛函的例子是所谓的机器f的“范”。“范”其实就是将f解读为无穷维空间的向量时f的“长度”的精致说法。对长度的这种解读与前面的弧长解读无关。它其实是通过推广熟悉的向量长度概念——受捷径公式启发——来定义无穷维中的“长度”概念。我们还没有见过这种特殊的同类相食机器，先花点时间搞清楚这种思想的来源，将有助于更好地理解在新的无穷维世界中所使用的推理方式。

[1] 澄清一下，我们在写F［f（x）］时之所以用方括号是因为（1）F（f（x））标记中的括号比较多，（2）写成F（f（x））可能显得机器f和F好像处于相同的抽象层面。虽然它们都是机器，虽然F［f（x）］中的方括号与圆括号起到的作用是一样的，标记的稍许差别还是能提醒我们f是吞进去一个数吐出来一个数的机器，而F则是吞进去整个机器吐出来一个数的机器。这是一个重要区别：虽然像f这样的普通函数也可以出现在像f（g（x））这样的项中，机器f还是只吞进去一个数（g在输入x时的输出），而F则是真正吞进去整台机器。F会捕食同类，f不会。