命题逻辑与命题演算

词项逻辑关注概念之间的关系，命题逻辑关注命题之间的关系。

在命题逻辑中，命题分为基本命题和复合命题。前面的AEIO是基本命题，所谓复合命题，是由两个以上的基本命题加上命题联结词构成的。比如“所有苹果都是食物，而且食物都可以吃”就是一个复合命题，“而且”就是命题联结词。除了“而且”，还有“并非”“或者”“如果……那么……”“等于”等。

人们需要命题逻辑，是为了在获知基本命题的真假之后，准确地判断一个复合命题的真假。就像人们需要词项逻辑穷尽词项间的推理规则一样，命题逻辑的野心也是要穷尽所有复合命题真假判断的规则。

他们又得逞了，用的同样是精密推演的思路。

例如，基本命题之一“所有苹果都是食物”，无论它的具体内容是什么，无非有真假两种可能性；基本命题之二“食物都可以吃”，同样也只有真假两种可能性。两个命题至多有四种组合：两者皆真，两者皆假，一真一假，一假一真。

既然基本命题的真假组合是有限的，是一个确定的排列组合，那么基本命题的内容就变得无关紧要了，我们就可以根据这个有限组合来穷尽所有复合命题的推出规律，最终明确各种命题联结词本身的逻辑内涵。

比如，在“而且”的联结下，只有两者皆真为真，其他情况都为假，意思是，只有当“所有苹果都是食物”和“食物都可以吃”这两个基本命题都是真命题时，“所有苹果都是食物，而且食物都可以吃”这句复合命题才是真的；在“或者”的联结下，只有两者皆假为假，其他情况都为真，意思是，只有当“所有苹果都是食物”和“食物都可以吃”这两个基本命题都是假命题的时候，“所有苹果都是食物，或者食物都可以吃”这句话才是假的，只要有一个基本命题是真的，这个由“或者”联结的复合命题就是真的。

由此，“而且”与“或者”这两个联结词的内涵与效用就被彻底澄清了。

逻辑学对联结词的精细梳理，基本符合我们的日常直觉，但也有反直觉的，比如“如果……那么……”这种。两个命题在“如果……那么……”的联结下，只有前真后假的情况下复合命题才为假，其他都为真，即便是前假后真，复合命题也依然为真。

举个例子，某天我发朋友圈宣称“如果今天天晴，那么我会出门”，但现实状况是，今天天气不好，但我依然出门了（前假后真），能证明我此前说了假话吗？并不能。我出门可以有很多理由，比如有事要办，要去吃饭。我们不能从后件的真伪来反推整个命题的真伪。天若下雨，地上会湿，但地上湿并不说明一定下过雨；敲击琴键，听见音乐，但音乐也可能来自播放器。现实世界的因果是复杂的，根据后件来判断前件的错误推理方式，被称作肯定后件谬误。与之相反，我们可以通过否定后件来判断整个命题的真伪，比如，我还是像前面那样宣称“如果今天天晴，那么我会出门”，可现实状况是今天明明天气很好，我却没有出门（前真后假），那么我无可争辩地说了假话，“如果今天天晴，那么我会出门”是假的，这在逻辑学中叫作否定后件推理。

两个基本命题，有4种真假组合状况，在数学上一共有16（2的4次方）种复合命题形式，它们的真假是可以被算出来的。

是的，算出来。前面说过，基本命题是真是假已经不重要了，所有可能的复合命题的真假状况，已经在数学的意义上提前穷尽了。

“在这里”“而且”“或”“如果……那么……”，这些联结词已经变成了有着特定结构的盒子，你朝它输入一些东西，它根据规则输出一些东西，变成了一种“函数”，由于输入、输出的值要么为真，要么为假，所以也叫真值函数。

命题下面这一堆真真假假，叫作真值表，这种对复合命题的数学化处理，叫命题演算。

你会疑惑，这种演算有什么意义？虽然在排列组合上有16种复合命题形式，但只有少数组合在日常语言中有效。比如，“真真真真”相当于说有这样一种联结词，无论你给出的简单命题是真是假，只要经由它联结，最终的复合命题永远是真的。日常语言中是找不到这种联结词的，逻辑似乎离生活越来越远了。

数学化的逻辑只是看似离我们越来越远了，某种质变正在悄然酝酿，并最终对人类文明产生了深远影响。

1854年，乔治·布尔出版了他的大作《思维规律的研究》，创立了逻辑代数。布尔发现，对逻辑命题的运算可以简化成对符号的代数运算。

真和假可以转换为1和0，“而且”可以直接转换为“逻辑乘法”：命题逻辑上的真真为真，相当于逻辑代数中的1×1=1；真假为假，相当于1×0=0。

“或者”就可以转换为“逻辑加法”：真假为真，相当于1+0=1；假真为真，相当于0+1=1。

“否定”则可以转换为“逻辑减法”（1减去）：否定真，得到假，相当于1-1=0；否定假，得到真，相当于1-0=1。

我们可以用这三个有限联结词的多次运算来表达所有联结词的功能。换句话说，“且”“或”“非”的多次组合，足以穷尽所有复合命题的可能形式。

比如我们可以用“否定”和“或”来替代“如果……那么……”。如果我们用自然语言来表述，“如果节目好看，则汤质很用心”这个复合命题就完全等价于“节目不好看，或者汤质很用心”，代数形式写作：P → Q= ┐P ∨ Q

换算方法：

我们知道“如果节目好看”和“汤质很用心”的真值组合如下图所示。

根据前面的知识，用“如果……那么……”联结，其复合命题的真值组合如下图所示。

我们需要让等号右边的联结词也得出同样的真值组合，此时就必须用到“否定”和“或者”。否定相当于逻辑减法，对“节目很好看”进行否定之后得到的命题“节目不好看”，其真值会完全相反。

此时，用联结词“或者”（逻辑加法）对“节目不好看”和“汤质很用心”这两个命题进行联结（运算），就会得到和“如果……那么……”联结词一模一样的真值结果：真假真真（1011）。

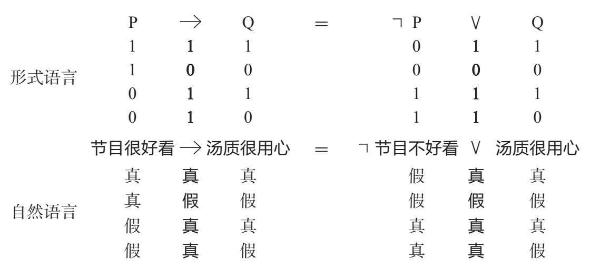
因此，我们才说“如果节目好看，则汤质很用心”和“节目不好看，或者汤质很用心”在逻辑上是完全等价的命题。生活中我们绝不会说“节目不好看，或者汤质很用心”这样的话，我们只要知道这是一种运算就够了。

正是这种运算使得用数学符号这样的形式语言来规范自然语言变成了一件可期的事，于是各路“大神”轮番登场。一方面，他们不断地在逻辑中加入新的要素，以求它能更好地消除语言和认知的模糊性；另一方面，他们不断拓展逻辑的应用场景，要求解决更多的现实问题，上一章提到的逻辑主义由此发轫，在20世纪初期盛极一时。

德国数学家弗雷格在命题逻辑中加入量词，开创了量化逻辑（谓词逻辑），并宣称能用它描述和分析所有数学上的、思想上的命题，伯特兰·罗素和怀特海在《数学原理》中试图用与、或、非三种逻辑为整个数学建立基础。

那段时间，世界上最聪明的头脑都参与了这场逻辑学革命，一场巨大的变革即将到来。