4.3　回顾

4.3　回顾

我不能接受。这个式子到底对不对呢？因为斐波那契数列可全都是整数哦，而通项公式里出现的 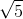$\sqrt{5}$ 真是令人匪夷所思。

米尔嘉却是一副很满足的样子，她喝着已经变冷的咖啡，听到我的疑问后说：“那你试着算算看喽？”

那么我就假设 n = 0, 1, 2, 3, 4，并分别将它们代入通项公式。

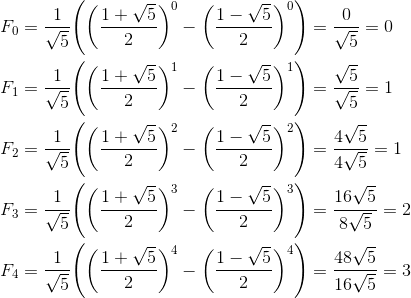
$\begin{aligned}&F_0=\frac{1}{\sqrt{5}}\Biggl(\biggl(\frac{1+\sqrt{5}}{2}\biggr)^0-\biggl(\frac{1-\sqrt{5}}{2}\biggr)^0\Biggr)=\frac{0}{\sqrt{5}}=0\\&F_1=\frac{1}{\sqrt{5}}\Biggl(\biggl(\frac{1+\sqrt{5}}{2}\biggr)^1-\biggl(\frac{1-\sqrt{5}}{2}\biggr)^1\Biggr)=\frac{\sqrt{5}}{\sqrt{5}}=1\\&F_2=\frac{1}{\sqrt{5}}\Biggl(\biggl(\frac{1+\sqrt{5}}{2}\biggr)^2-\biggl(\frac{1-\sqrt{5}}{2}\biggr)^2\Biggr)=\frac{4\sqrt{5}}{4\sqrt{5}}=1\\&F_3=\frac{1}{\sqrt{5}}\Biggl(\biggl(\frac{1+\sqrt{5}}{2}\biggr)^3-\biggl(\frac{1-\sqrt{5}}{2}\biggr)^3\Biggr)=\frac{16\sqrt{5}}{8\sqrt{5}}=2\\&F_4=\frac{1}{\sqrt{5}}\Biggl(\biggl(\frac{1+\sqrt{5}}{2}\biggr)^4-\biggl(\frac{1-\sqrt{5}}{2}\biggr)^4\Biggr)=\frac{48\sqrt{5}}{16\sqrt{5}}=3\\\end{aligned}$

最后得出的答案是 0, 1, 1, 2, 3，确实都是斐波那契数列中的数字。啊，原来如此，当代入具体数字时，分子分母都有 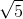$\sqrt{5}$ ，所以可以互相抵消。

哇，实在是太厉害了！我也喝起了咖啡，一边喝一边开始回想今天所做的事情：我们一开始的目标是要求斐波那契数列的通项公式。为此，我进行了以下三步。

（1）思考将 xn 的项的系数用斐波那契数列的通项 Fn 来表示的生成函数 F(x)。

（2）求生成函数 F(x) 的有限项代数式（这里是关于 x 的有限项代数式）。这时，可以运用斐波那契数列的推导公式来求解。

（3）用无穷级数的形式来表达函数 F(x) 的有限项代数式。这时 xn 项的系数就是斐波那契数列的通项公式。

综上所述，从将函数的系数用通项 Fn 来表示，到求出生成函数，这就是“抓住了求解数列的关键”。原来如此……但是，真是“路漫漫其修远兮”啊……

“求斐波那契数列的通项公式”的“旅行地图”

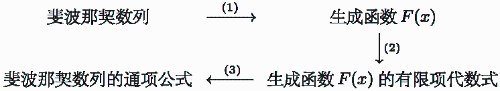
米尔嘉又说：“生成函数是求解数列最有效的方法。为什么这么说呢？因为当我们在生成函数王国漫步的时候，我们所知道的关于函数的解析技巧对求解很有帮助。做函数题时总结出来的方法在数列问题上也有了用武之地。”

我听了米尔嘉的话后又开始担心起别的事情。在计算无穷级数的时候，我们改变了求和的顺序，应该没什么问题吧？到底会不会有关系呢？

“如果在条件里不说清楚的话就不行，但这次没关系。先不告诉别人我们是用生成函数的方法求得通项公式的，然后我们用数学归纳法来证明一下所得到的通项公式就可以了。”米尔嘉像完成件大事一样，轻松地说。

……一直以来我都在做公式的展开，

这是为了运用生成函数这一重要的解题方法

来展现发现等式关系的方法。

——高德纳，《计算机程序设计艺术》[22]

4.3 回顾

4.3　回顾