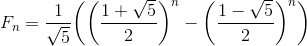4.2.1 斐波那契数列
我们转移到附近的咖啡店,草草点完单后又继续开始刚才的数列的话题。抓住数列的要害究竟是怎么回事呢?两个王国又到底是什么呢?听了我的问题,米尔嘉推了推眼镜说:“嗯,是啊。”
4.2.1 斐波那契数列是啊。这个比喻可能不太符合逻辑,太夸张了。“在两个王国里穿梭漫步,抓住数列的要害”其实就是“运用生成函数来求数列的通项”呀。
现在给你看看“旅行地图”吧。首先,求得与数列相对应的生成函数。其次,将生成函数变形,求出生成函数的有限项代数式。然后再将有限项式根据幂级数展开,最终求得数列的通项。也就是说,通过生成函数来找出数列的通项。
“运用生成函数来求数列的通项”的“旅行地图”

例如,以数列中的斐波那契数列为例。你知道斐波那契数列吧?
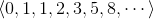
这个数列从第三项开始,每一项都等于前两项之和。
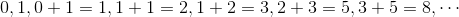
这个数列也有从 1 开始的情况,但是这里我们从 0 开始。
我们假设 Fn 为斐波那契数列的通项。F0 和 0 相等,F1 和 1 相等,当 n ≥ 2 时,则 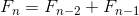 ,所以 Fn 就被定义为表示各项间关系的推导公式。
,所以 Fn 就被定义为表示各项间关系的推导公式。
斐波那契数列的定义(推导公式)
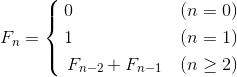
“从第三项开始,每一项都等于前两项之和”——斐波那契数列的这个性质在这个定义中得到了充分的体现。另外,还可以像 F0, F1, F2, ... 这样计算出斐波那契数列。但是,Fn 没有表现为“关于 n 的有限项代数式”。也就是说,通项公式 Fn 中并未使用 n,不是关于 n 的直接代数式。这也就是我所说的“没有抓住数列的要害”状态。
现在我们假设要求斐波那契数列的第 1000 项是多少。一般情况下,我们就用 F0 + F1 来求 F2,用 F1 + F2 来求 F3,…… 如此重复计算后,最后通过求 F998 + F999 的和才能算出 F1000 的值。如果靠推导公式来计算 Fn 的话,那么要进行 n - 1 次加法计算。这实在太无聊了。我想将 Fn 表示成“关于 n 的有限项代数式”。“关于 n 的有限项代数式”究竟是什么意思呢?粗略地说,它就是“将大家都知道的运算方法在有限的次数内进行组合后得到的代数式”。
我很想将 Fn 表示成“关于 n 的有限项代数式”,抓住斐波那契数列的要害。
问题 4-1
将斐波那契数列的通项 Fn 表示成“关于 n 的有限项代数式”。
4.2.2 斐波那契数列的生成函数那么,接下来我们就将与斐波那契数列相对应的生成函数称为 F(x)。也就是说,我们将其对应关系表现为以下形式。
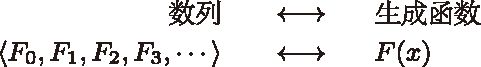
在函数 F(x) 中,如果将 xn 这一项的系数用 Fn 来表示,那么整个函数就可以用以下式子表示出来。这样,我们就可以向生成函数的王国过渡了。
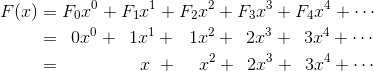
接下来,我想调查一下函数 F(x) 的性质。函数 F(x) 的系数 Fn 是斐波那契数列的通项,如果好好利用这点的话,我们很快就能找到关于函数 F(x) 的有趣性质。
斐波那契数列的性质究竟是什么呢?当然我们刚才已经求得推导公式 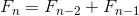 ,如果我们好好利用这个表示各项间关系的推导公式的话,
,如果我们好好利用这个表示各项间关系的推导公式的话,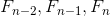 这样的系数就可以在 F(x) 的计算过程中出现。如下所示。
这样的系数就可以在 F(x) 的计算过程中出现。如下所示。
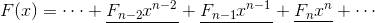
我想把系数 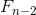 和
和 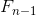 相加试试看,但是 x 的幂次方互不相同,所以不能合并同类项。那该怎么办呢?
相加试试看,但是 x 的幂次方互不相同,所以不能合并同类项。那该怎么办呢?
◎ ◎ ◎
米尔嘉看看我。嗯。x 的幂次方确实不同,不能将它们的系数直接相加。因为它们不是同类项,所以不能合并。将数列和生成函数相互对应,真的会发生有趣的现象吗?——终于,从米尔嘉嘴里吐出了一句:“很简单哦。”
4.2.3 封闭表达式很简单哦。
x 的幂次方如果互不相同的话,将不同的部分乘上 x 就好了。同底数幂相乘,底数不变指数相加,也就是所谓的指数运算法则。
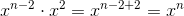
例如,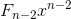 乘以 x2 的话得
乘以 x2 的话得 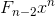 。如下所示,如果巧妙地进行乘法运算的话,就可以统一为 xn 的形式。为了使形式统一,我们将 1 写作 x0。
。如下所示,如果巧妙地进行乘法运算的话,就可以统一为 xn 的形式。为了使形式统一,我们将 1 写作 x0。
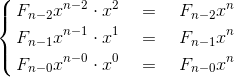
这样一来,我们就可以运用与函数 F(x) 相对应的斐波那契数列的推导公式了。好,我们将 F(x) 分别和 x2, x1, x0 相乘后的式子写下来看看。
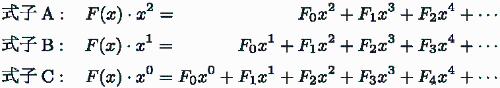
这样就统一了幂次项。利用式子 A、式子 B、式子 C,我们接着进行计算。这样一来,我们就可以运用同类项系数 Fn 的推导公式。
式子A +式子B -式子C
在进行计算的时候,式子左边就变成了以下形式。
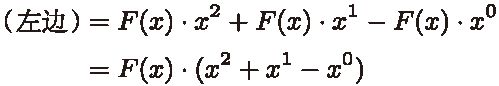
然后,式子右边变为以下形式。
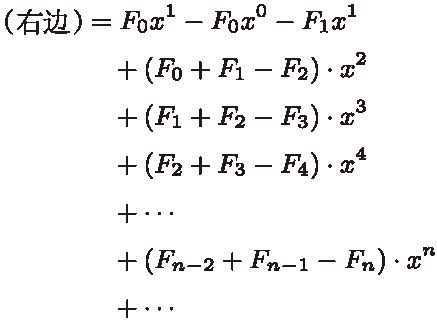
式子右边经计算就只剩下起始部分 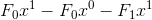 ,其他部分全都抵消了。为什么这么说呢?这是因为根据斐波那契数列的推导公式,
,其他部分全都抵消了。为什么这么说呢?这是因为根据斐波那契数列的推导公式,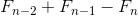 这部分等于 0,任何数乘以 0 都会马上消失。
这部分等于 0,任何数乘以 0 都会马上消失。
我们已经没什么必要写成 x0 和 x1 的形式了,直接写 1 和 x 就可以了。那么,F0 就可以写成 0,F1 就可以写成 1。于是,我们得到了以下式子。
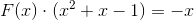
两边同时除以 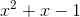 ,整理后就能求得 F(x) 的有限项代数式。这就是 F(x) 的庐山真面目哦。
,整理后就能求得 F(x) 的有限项代数式。这就是 F(x) 的庐山真面目哦。
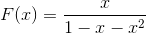
我看到斐波那契数列的生成函数变形成了这样一个简单的有限项代数式,心中雀跃无比。因为这个代数式包括了无限延续下去的斐波那契数列的全部内容,是一个高度浓缩的式子。
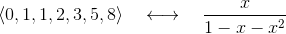
斐波那契数列的生成函数 F(x) 的封闭表达式
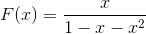
我们思考讨论了斐波那契数列的生成函数 F(x)。如果用 x 来表示 F(x) 的有限项代数式,x 的 n 次方前的系数应该是 Fn。
所以,接下来我们的目标是想办法将 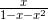 用 x 的无穷级数来表示。
用 x 的无穷级数来表示。
我们曾经用下面的分式形式来表现过关于 x 的无穷级数。
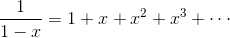
比如说,我们能否想办法将 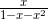 变成与
变成与 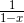 类似的形式呢?如果可能的话,我们就能从生成函数的王国回到数列的王国了。回去的时候当然不能空手,请带一件生成函数王国的“土特产”噢。那就是斐波那契数列的通项公式。你觉得如何?
类似的形式呢?如果可能的话,我们就能从生成函数的王国回到数列的王国了。回去的时候当然不能空手,请带一件生成函数王国的“土特产”噢。那就是斐波那契数列的通项公式。你觉得如何?
◎ ◎ ◎
米尔嘉盯着我的眼睛。啊,对了,接下来只要把生成函数 F(x) 写成无穷级数的形式,就可以求得斐波那契数列的通项公式了吧。我一直盯着生成函数的形式看,彻底弄清了其结构。
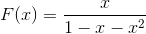
分母 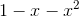 是个二次代数式。首先,先试试将
是个二次代数式。首先,先试试将 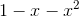 因式分解。我在练习本上又开始计算起来。米尔嘉一直在旁边盯着看。
因式分解。我在练习本上又开始计算起来。米尔嘉一直在旁边盯着看。
假设有未知常数 r 和 s,式子 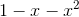 便可分解成以下形式。
便可分解成以下形式。
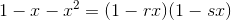
如果照上述式子那样分解的话,通过求下面式子的分数和,在通分的时候分母就正好可以变形成 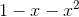 的形式了。
的形式了。
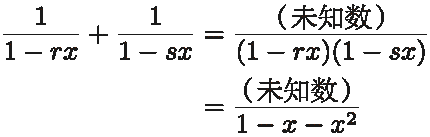
计算这个式子,当它变形成 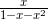 的形式后,再求出 r 和 s 就可以了。
的形式后,再求出 r 和 s 就可以了。
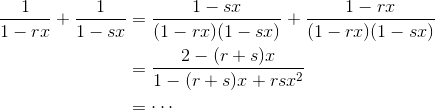
嗯,只要我们顺利计算出 r 和 s 的值,分母 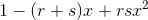 就有可能变成
就有可能变成 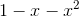 的形式。但是,分子
的形式。但是,分子 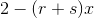 却很难变形为 x 的形式,因为常数 2 无法被抵消。
却很难变形为 x 的形式,因为常数 2 无法被抵消。
当我在嘀咕时,米尔嘉在一旁提示说:“如果用这种方法,就能顺利进行下去哦。”
4.2.5 解决如果用这种方法,就能顺利进行下去哦。
我们在分子里放入参数。也就是说,假设有 4 个未知常数 R,S,r,s,接着思考以下式子就好了。
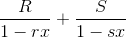
计算此式。
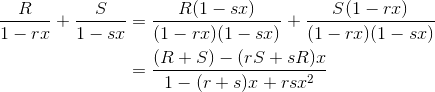
如果要使以下式子成立,只要确定常数 R,S,r,s 分别为多少就可以了。
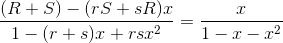
比较等式左右两边后,只要解出以下联立方程组就可以了。
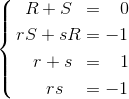
4 个未知数配有 4 个独立的等式。我们试着解一下这个联立方程组。
首先,将 R 和 S 分别转化成只含有 r 和 s 的关系式。
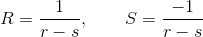
这样一来,就找到了用无穷级数来表示 F(x) 的头绪。我们先暂且不求出 r 和 s 具体为多少,继续推导下去。
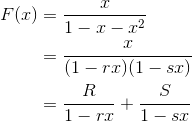
这里将 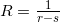 ,
,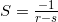 代入。
代入。
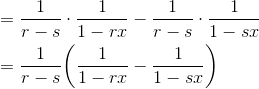
再将 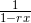 用
用 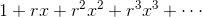 代入,将
代入,将 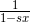 用
用 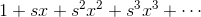 代入。
代入。
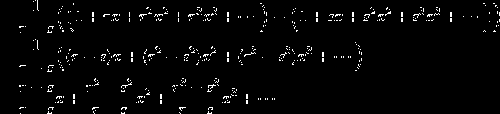
然后整理一下。
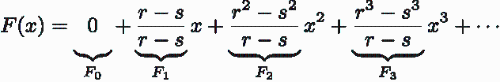
于是,我们就求得了用 r 和 s 所表示的斐波那契数列的通项公式。
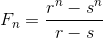
接下来只剩计算 r 和 s 的值这一步了。关于 r 和 s 的联立方程组为
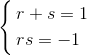
用通常解联立方程组的方法当然也可以,不过既然 r、s 的和为 1,积为 -1,那么就可以说它们是方程 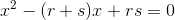 的解。也就是说,解这道题的关键就是要知道“一元二次方程的解与系数的关系”。为什么这么说呢?因为我们可以将这个一元二次方程分解为以下形式。
的解。也就是说,解这道题的关键就是要知道“一元二次方程的解与系数的关系”。为什么这么说呢?因为我们可以将这个一元二次方程分解为以下形式。
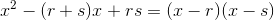
换句话说,根据 r + s = 1,rs = -1 这个条件,我们可以得出二次方程的解就是 r 和 s。
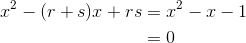
运用一元二次方程的求根公式可以得到 x 的值。
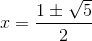
假设 r 大于 s,可得
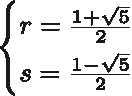
因为 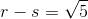 ,所以
,所以
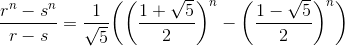
因此,我们就能求出斐波那契数列的通项公式了,如下所示。
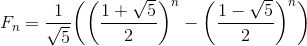
好了,这样问题就告一段落了。
解答 4-1 (斐波那契数列的通项公式)