6.8.2 设计曲线的理想形状

6.8.2　设计曲线的理想形状

有了以上因素，就可以进行数值设计了。我们先做各个变量的定义域设计、值域设计、锚点设计。

●定义域设计：即函数输入的数值范围是多少，比如阅读时长的定义域为［0,+∞)、阅读百分比的定义域为［0,1］、阅读章节数的定义域为{x|x∈Z且x>0}。

●值域设计：即函数输出的数值范围是多少，本例中的输出值的值域为［0,1］。

●锚点设计：即函数给定输入以后，期望输出是多少，一般需要指定边界值，如表6-5所示。

表6-5　锚点设计与边界值定义举例

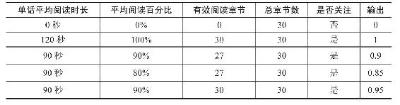
表6-5所示的数据仅供参考，笔者在设计锚点的时候往往会改变其中的一个变量，控制其他变量不变，给出多组输出值，根据输出值在纸上描绘出期望的曲线形状。

接下来构造设计公式。在设计数据公式时一般有两种加权方式，分别是线性加权和非线性加权，其中线性加权适用于多数情况。

●线性加权：大多数情况适用，即构造y=k1x1+k2x2+…+knxn的形式，ki为线性加权的权重参数，xi为输入值。优点是权重的调整可理解性强，随着自变量变化比较容易预测到因变量的变化。

●非线性加权：少数情况适用，实际操作中一般会先进行调研（即类似场景下的公式、历史项目中有无经验可以借鉴），然后对之前的公式做改进。常见的函数形式如下。

　•对数函数：对数函数是非线性函数中最经常使用的，一般会选取log10(1+x)或者loge(e+x)的数值形式。

　•三角函数：笔者最常用的是y=Tanh(x)函数。

　•Sigmoid函数：函数形式为y=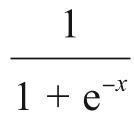，输入值的定义域是实数，输出值的值域是（0，1）。

　•zScore函数：对输入值定义域进行数值标准化操作，公式为x′i=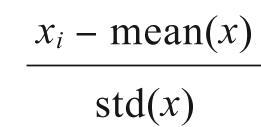。因为均值和方差属于样本的描述型统计量，所以zScore函数得到的数值并非绝对数值。

一般情况下，笔者选择的最终函数形式类似于f(xi,y)=(k1x1+k2x2)logk3(1+y)，这种公式相对普适。

之后就可以使用数学软件进行参数拟合并绘制曲线图了。笔者推荐使用Python包或者Matlab的curvefit工具箱。Python更通用，但配置环境难度大一些。Matlab在科学计算上是佼佼者，在数值设计时往往选择Matlab。上述数学软件均支持自行设定函数形式、自行设定输入值和输出值，程序会经过数值算法得到目标参数值。下列代码为使用Python语言进行函数拟合的实例。

from scipy.optimize import curve_fit
import numpy as np
x = np.arange(1, 17, 1)
y = np.array([4.00, 6.40, 8.00, 8.80, 9.22, 9.50, 9.70, 9.86, 10.00,10.20, 10.32, 10.42, 10.50, 10.55, 10.58, 10.60])
def func(x,a,b):
      return a*np.exp(b/x)
popt, pcov = curve_fit(func, x, y)
a=popt[0]
b=popt[1]

上述代码拟合了y=aeb/x的函数形式，并给出了期望的输入值和输出值，使用Python工具包scipy.optimize中的curve_fit函数就可以求解出a和b的参数值。

谨记高中函数口诀中的“左加右减，上加下减”进行自变量的加减调节。最后，绘制图形是必须的步骤，以检验目标函数值是否符合预期。

当存在多个因素时，逐个控制其他因素不变，看单个自变量对因变量的影响，此时图形为2D图形，也可以选择两个自变量对因变量的影响，直接绘制三维曲线图形。