参考文献和导读
我把书库的钥匙给你，
不够的话就去图书馆吧。
你想知道的答案一半都在书里。
只有一半？那剩下的一半呢？
还无人知晓。
—— 坂田靖子《巴基尔的优雅生活》
读物
[1] 結城浩 , 『数学ガール』1, ソフトバンククリエイティブ , ISBN978-4-7973-4127-9， 2007 年
1中文版名为《数学女孩》，朱一飞译，人民邮电出版社，2015 年。—— 译者注
这本读物描写了我、米尔嘉以及泰朵拉三人的邂逅和故事。我们三个高中生在放学后的图书室、教室以及咖啡店挑战与学校所学内容略有不同的数学。
[2] Simon Singh， 青木薫訳，『フェルマーの最終定理——ピュタゴラスに始まり、ワイルズが証明するまで』2， 新潮社， SBN4-10-539301-4， 2000 年
2中文版名为《费马大定理：一个困惑了世间智者 358 年的谜》，薛密译，广西师范大学出版社，2013 年。—— 译者注
这本读物戏剧性地阐述了从费马大定理诞生到怀尔斯证明费马大定理之间的一系列故事。特别是对怀尔斯发现已公布的证明有疏漏，随后突破难关这部分的描写最是精彩。本书的文库版由新潮文库出版。
[3] 高木貞治， 『近世数学史談』， 岩波書店， ISBN4-00-339391-0， 1995 年
这本读物生动有趣地记录了高斯、柯西、狄利克雷、伽罗瓦、阿贝尔等众多数学家的一生及其建树。
面向高中生[4] 松田修 + 津山工業高等専門学校数学クラブ， 『11 からはじまる数学― k ‐ パスカル三角形、 k ‐ フィボナッチ数列、 超黄金数』， 東京図書，ISBN978-4-489-02027-8， 2008 年
本书中描写了四位高专生 3 在“数学俱乐部”里进行的数学研究，也就是真实世界中的数学男孩和数学女孩们关于帕斯卡三角形和斐波那契数列进行的研究。对于那些想凭自己的能力开始研究数学的高中生以及教师们，这本书想必会有很大的帮助（参考：第 7 章末尾的引用）。
3相当于中国的职高生。—— 译者注
[5] 芹沢正三， 『素数入門—— 計算しながら理解できる』， 講談社， ISBN4-06-257386-5， 2002 年 （正誤表 http://shop.kodansha.jp/bc/books/bluebacks/images/seigo.pdf ）
本书中记述了许多初等整数论的具体问题，是一本能够一边读一边自己进行计算和论证的好书（参考：第 7 章的群·环·域的记述）。
[6] 黒川信重， 『オイラー、 リーマン、 ラマヌジャン』， 岩波書店， ISBN4-00-007466-0， 2006 年
本书中以欧拉、黎曼、拉玛努扬三人为主题，讲述了不可思议的 Zeta 世 界（参 考：第 10 章棱镜的比 喻、代数 Zeta 和解析 Zeta）。
[7] 小林昭七， 『なっとくするオイラーとフェルマー』， 講談社， ISBN4-06-154537-X， 2003 年
本书中收集了许多关于数论的有趣话题（参考：第 8 章 FLT(4) 的证明）。
[8] 足立恒雄， 『フェルマーの大定理が解けた！』， 講談社， ISBN4-06-257074-2， 1995 年
本书中用椭圆曲线的观点总结了费马大定理。虽然里面有不少数学公式，不过作者下了一番功夫，所以即使抛开这些数学公式，读者也能掌握大体流程（参考：第 2 章单位圆和勾股数的关系）。
[9] 足立恒雄， 『フェルマーの大定理 —— 整数論の源流』， 筑摩書房 （ちくま学芸文庫）， ISBN4-480-09012-6， 2006 年
本书中描绘了数学家的人物肖像、历史背景及数学内容，多方位地描述了费马大定理。作者绝妙地拿捏了记述数学的火候，也很适合对数学性文章抱有兴趣的读者一读（参考：第 10 章费马大定理的历史）。
[10] 足立恒雄， 『フェルマーを読む』， 日本評論社， ISBN4-535-78153-2， 1986 年
本书中解释了费马在丢番图 的《算 术》一 书中写下的 48 项内容（参考：第 10 章《算术》的解释）。
[11] 志賀浩二， 『数学が育っていく物語 （第 2 週）—— 解析性 実数から複素数へ』， 岩波書店， ISBN4-00-007912-3， 1994 年
本书中以老师和学生的对话形式来讲述数学，同时也涉及了数学家的人格，是一本能够让人静下心来慢慢阅读的数学书（参考：第 5 章的复数）。
[12] 矢野健太郎＋高橋正明， 『改訂版 複素数 （モノグラフ 9）』， 科学新興新社， ISBN4-89428-166-X， 1990 年
这是一本面向高中生的参考书。此专题著作系列适合对特定主题抱有兴趣的高中生钻研学习（参考：第 5 章复数的积）。
[13] 福田邦彦＋石井俊全， 『数学を決める論証力』， 東京出版， ISBN4-88742-048-X， 2001 年
这是一本培养证明能力的参考书。除了介绍反证法和数学归纳法这些著名的证明方法外，还讲解了一些考生容易栽跟头的证明题的错误所在（参考：第 4 章用另一种证明法来证明是无理数）。
[14] 栗田哲也＋福田邦彦， 『マスター· オブ · 整数』， 東京出版， ISBN4-88742-017-X， 1998 年
本书中为大家讲解了质因数分解、最大公约数、欧拉函数、互质和勾股数等关于整数的话题（参考：第 4 章用另一种证明法来证明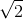 
是无理数、第 5 章的格点问题）。
[15] 吉田武，『虚数の情緒——中学生からの全方位独学法』，東海大学出版会，ISBN4-486-01485-5， 2000 年
本书是一部以数学和物理为中心，引导读者从基础开始积极动手学习的大作，有着惊人的趣味性。
面向大学生[16] 『岩波数学入門辞典』， 岩波書店， ISBN4-00-080209-7， 2005 年一本简明易懂地讲解了数学专门用语的词典。
[17] 高木貞治，『初等整数論講義 第 2 版』，共立出版，ISBN4-320-01001-9， 1971 年
一本讲解古典整数论的书。
[18] 加藤和也， 『解決！フェルマーの最終定理—— 現代数論の軌跡』， 日本評論社， ISBN4-535-78223-7， 1995 年
本书中讲解了费马大定理和与其有关的数学知识。本书中总结了月刊杂志《数学研讨会》的连载内容，通过丰富多彩的比喻和故事来谈论高深的数学，读者可以通过本书生动形象地认识与把握数学。
[19] 藤崎源二郎＋森田康夫＋山本芳彦， 『数論への出発 増補版』， 日本評論社， ISBN4-535-78362-4， 2004 年
本书中将初等整数论到费马大定理简洁地加以了总结（参考：第 10 章）。
[20] Ronald L. Graham， Donald E. Knuth， Oren Patashnik ，有沢誠 ＋ 萩野達也＋安村通晃＋石畑清訳，『コンピュータの数学』4， 共立出版，ISBN4-320-02668-3， 1993 年
4中文版名 为《具体数学：计算机科学基础》，张明尧、张凡译，人民邮电出版社，2013 年。—— 译者注
这是一本以求和为主题的离散数学的书（参考：第 3 章质数指数记数法、a ⊥ b 的形式）。
[21] David Gries， Fred B. Schneider， 『コンピュータのための数学 —— 論理的アプローチ』5， 日本評論社， ISBN4-535-78301-2， 2001 年
5英文原版名为 A Logical Approach to Discrete Math，Springer，1993 年。—— 译者注
一本讲解离散数学的书，目标是使读者掌握逻辑，将其作为思考的工具。
[22] Philip J.Davis， Reuben Hersh， 柴垣和三雄＋田中裕＋清水邦夫訳，『数学的経験』6， 森北出版， ISBN4-627-05210-3， 1986 年
6中文版名为《数学经验（学习版）》，王前译，大连理工大学出版社，2013 年。—— 译者注
一本从多个角度汇集了各种数学话题的读物。话题涵盖范围太广，所以有一些难以读懂的部分，不过也包含一些引人深思的内容。
[23] Joseph H. Silverman， John Tate， 足立恒雄訳，『楕円曲線論入門』7， シュプリンガー · フェアラーク東京， ISBN4-431-70683-6， 1995 年
7英文原版名为 Rational Pointson Elliptic Curves，Springer，1994 年。—— 译者注
一本椭圆曲线的入门书，把焦点放在了数论的侧面。
[24] Leonhard Euler， 高 瀬正仁訳， 『オ イ ラーの 解析 幾何』8， 海鳴社，ISBN4-87525-227-7， 2005 年
8英文原版名为 Introductio in Analysin Infinitorum，1748 年。—— 译者注
一本莱昂哈德·欧拉自己编写的几何书。读者可以通过欧拉自己写的文章品味有关坐标、曲线以及函数的知识。书中出现了许多具体例子，从这点可以看出欧拉非常重视具体例子。
面向研究生和专家[25] 加藤和也＋黒川信重＋斉藤毅， 『数論Ⅰ—— Fermat の夢と類体論』，岩波書店， ISBN4-00-005527-5， 2005 年
这是一本数论的教科书。作者下了许多功夫，为的是让读者一边学习真正的数学，一边体验数字的不可思议及惊奇之处。这本书在笔者编写本书的过程中给了笔者很大的帮助（参考：第 2 到第 4 章、第 7 章、第 10 章的结构）。
[26] 黒川信重＋栗原将人＋斉藤毅， 『数論Ⅱ—— 岩澤理論と保型形式』，岩波書店， ISBN4-00-005528-3， 2005 年
上述《数论Ⅰ》的续作（参考：第 2 到第 4 章、第 7 章、第 10 章的结构）。
[27] 谷山豊，『谷山豊全集[増補版]』， 日本評論社， ISBN4-535-78209-1， 1994 年
创造谷山 - 志村定理的谷山丰的全集著作。集合了谷山丰的论文、评论、随笔和书信等，此外还收录了作为“谷山 - 志村定理”被公式化的谷山的问题。
[28] Andrew Wiles ， “ Modular Elliptic Curves and Fermat's Last Theorem ”， The Annals of mathematics ， 2nd Ser. ， Vol. 141 ， No.3 （May， 1995）， pp.443-551
怀尔斯的论文，这篇论文证明了费马大定理。论文总计 109 页，一共 5 章。假如费马的证明过程跟怀尔斯一样，那这么多的过程，空白处确实是写不下啊。
网络资料[29] http://itsoc.org/review/05pl1.pdf ， Gerhard Frey ， “ The Way to the Proof of Fermat's Last Theorem”
讲述了想出弗赖曲线的 Gerhard Frey 如何解决费马大定理的历史（参考：第 10 章的结构）。
[30] http://www.hyuki.com/girl/, 結城浩 ,『数学ガール』
汇集了诸多关于数学和女孩的读物。《数学女孩》的最新信息也在这里。
“出于兴趣读的书反而更难，真怪。”
“因为自己喜欢的书都是拿来挑战自己理解极限的嘛。”
——《数学女孩：费马大定理》[30]