7.3 除法的本质
夜晚,我的房间。
“学这么晚辛苦了。”我妈放下了一杯可可。
已经这么晚了吗……我看着马克杯,恍惚地想着。说过了喝咖啡就行,她却总拿来可可,能不能别总是把我当小孩子看啊。
我爸和我妈结婚后有了我,一家人。米尔嘉也有家人,泰朵拉也有家人。
我们才十来岁,但我们也背负着许多东西,某些我们要背负的东西。
米尔嘉也是。
“不过,哥哥他在我小学三年级的时候就……死了。”
泰朵拉也是。
“所以,所以……请你不要回头。”
——我后背上能感觉到泰朵拉的双手在不停颤抖。我的心也忐忑不定。
唉。
我翻开笔记本。
数学……
数学的存在很有分量 —— 我一直这么想。或许完成后的数学确实是这样,但完成之前的数学肯定有所不同。
写数学公式,就会留下数学公式。半途而废,就只会留下写到一半的数学公式。这是理所当然的。
然而,教科书上没有写到一半的数学公式。在建筑工地上已经搭好了脚手架。所以一说到数学,我们脑海中总会浮现出整然有序的、已经完成的画面。但实际上,那些创造出最尖端数学的地方,不都是跟施工现场一样乱七八糟的吗?
毕竟发现数学、创造数学的是人类,怀着残缺、震颤、忐忑之心的人类。是憧憬美丽的结构,倾慕永恒,想方设法捕捉无限的人类,培育出了今日的数学。
不是纯粹地获取,而是由自己创造出来的;从搜集不起眼的水晶碎片开始,直至建成宏伟的佛寺;在一无所有的空间里放入公理,由公理推导定理,由定理再导出其他定理;由一颗小小的种子开始,构建整个宇宙。 —— 这就是数学。
米尔嘉优雅的解答,泰朵拉付出的努力,尤里对于条件的关注……我能改变对数学的固有印象,也是受了她们的巨大影响啊。
我喝着热乎乎的可可,漫无边际地想着。
7.3.2 运算表的研究那么,该研究数学了。
泰朵拉把 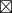 的运算表写到一半,那我也来写写看吧。
的运算表写到一半,那我也来写写看吧。
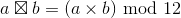
只是做个乘法运算,写出除以 12 的余数而已,费不了什么工夫。

不过,米尔嘉为什么让泰朵拉写这个运算表呢?一切得从在同余式的两边同时除以 C 这里说起。
问题7-1 (同余式和除法运算)
假设 a, b, C, m 为整数。
当 C 具有何种性质时,以下关系成立?
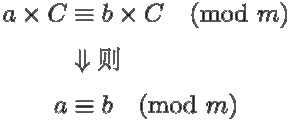
米尔嘉说了。
“观察乘法运算不是没用的,它能帮你更好地理解除法运算。”
好,那我就举 m = 12 这个例子,来好好观察一下这个运算表。
一行一行地读。
因为 0 乘以什么数字都得 0,所以 0 这行全部是 0。
1 这行是 0, 1, 2, ... , 11,数字依次排列。这也是理所当然的。
2 这行是 0, 2, 4, 6, 8,直到 10 数字是递增的,但是当 a × b 等于 12 的时候又归零了。因为这是以 12 为模的运算 —— 也就是说取除以 12 的余数,所以也是很自然的。
3 这行也一样。0, 3, 6,直到 9,当 a × b 等于 12 的时候又归零。
嗯……同余式
a × C ≡ b × C (mod 12)
用运算 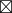 可以写成下面这样。
可以写成下面这样。
a 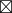 C = b
C = b 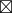 C
C
因为 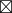 里已经包含了 mod 的计算,所以不写 ≡,写成 = 就可以。
里已经包含了 mod 的计算,所以不写 ≡,写成 = 就可以。
嗯……那么接下来就要思考 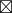 的逆运算了吗。
的逆运算了吗。
……
不,不对,搞错了。
与其综合考虑在集合 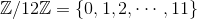 中
中 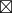 的逆运算,不是应该先考虑 C 的逆元吗?假设 C 的逆元为 C' ,C' 就满足
的逆运算,不是应该先考虑 C 的逆元吗?假设 C 的逆元为 C' ,C' 就满足
C 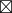 C' = 1
C' = 1
如果集合 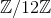 内存在这样的数字 C',就应该能进行“除法运算”。因为在
内存在这样的数字 C',就应该能进行“除法运算”。因为在
a 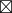 C = b
C = b 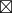 C
C
的两边同时乘以 C',就存在以下等式。
(a 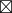 C)
C) 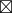 C' = (b
C' = (b 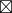 C)
C) 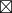 C'
C'
因为 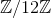 关于
关于 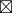 满足结合律,所以上面的式子可以写成下面这样。
满足结合律,所以上面的式子可以写成下面这样。
a 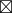 (C
(C 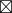 C') = b
C') = b 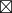 (C
(C 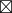 C')
C')
因为 C 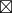 C' = 1,所以
C' = 1,所以
a 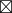 1 = b
1 = b 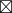 1
1
运用运算 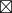 的定义,可以写成以下这样。
的定义,可以写成以下这样。
(a × 1) mod 12 = (b × 1) mod 12
即
a mod 12 = b mod 12
由此,以下式子成立。
a ≡ b (mod 12)
也就是说,如果对于 C 存在逆元 C',那么就可以在同余式的两边同时除以 C 不是吗?
嗯嗯,总而言之,除以 C 和乘以它的倒数 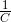 是一回事。这样就不是普通的除法运算,而是考虑到 mod 的除法运算了。从这个角度来说,把 C 的逆元写成 C',可能不如象征性地写成
是一回事。这样就不是普通的除法运算,而是考虑到 mod 的除法运算了。从这个角度来说,把 C 的逆元写成 C',可能不如象征性地写成 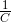 或者 C-1 比较好。
或者 C-1 比较好。
来找 C 的逆元存在的条件吧。从 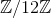 里找出满足 C
里找出满足 C 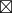 C' = 1 的数字就行。怎么找好呢……啊,这样啊!很简单,用运算表就行了!只要找出表中含有 1 的行就可以。哈哈,所以米尔嘉才让泰朵拉写运算表的啊……
C' = 1 的数字就行。怎么找好呢……啊,这样啊!很简单,用运算表就行了!只要找出表中含有 1 的行就可以。哈哈,所以米尔嘉才让泰朵拉写运算表的啊……
那么,我们把运算表中 1 的地方画上圆圈。

咦?没想到这么少。存在逆元的只有 1, 5, 7, 11 这四个吗……嗯?
1, 5, 7, 11 ?
1, 5, 7, 11 不是之前在时钟巡回里常见的“与 12 互质的数字”吗?!
也就是说,和 12 互质的数字关于 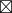 存在逆元。换句话说,只要是跟模互质的数字,就可以进行除法运算……就是这么回事吧?
存在逆元。换句话说,只要是跟模互质的数字,就可以进行除法运算……就是这么回事吧?
说起来,米尔嘉在学校出的例子真有意思啊!—— 15 和 75 以 12 为模同余。

不出所料。除以跟 12 互质的 5,结果仍然同余。然而除以跟 12 不互质的 3,同余就不成立了。
7.3.3 证明我试着写下刚刚根据运算表得到的猜想。
猜想:同余式中,用与模互质的数字可以进行除法运算。也就是说,当以下式子成立时,
a × C ≡ b × C (mod m)
若 C 与 m 互质(即 C ⊥ m),则以下式子成立。
a ≡ b (mod m)
好的,试着证明这个猜想吧。因为可以写出 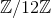 的具体运算表,所以可以检验。但通常情况下,
的具体运算表,所以可以检验。但通常情况下,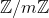 包含无数个元素,写不出具体的运算表,所以必须严谨地证明。
包含无数个元素,写不出具体的运算表,所以必须严谨地证明。
从这里出发。
a × C ≡ b × C (mod m)
这个式子可以变形成以下这种形式。
a × C - b × C ≡ 0 (mod m)
左边提出 C,得到以下式子。
(a - b) × C ≡ 0 (mod m)
以 m 为模,(a - b) × C 与 0 同余,说明 (a - b) × C 是 m 的倍数。也就是说,存在某个整数 J,使得以下等式成立。
(a - b) × C ≡ J × m
这样一来,所有字母都是整数,且两边都变成了积的形式。
我想推导的是,存在某个整数 K,使得以下等式成立。
a × b = K × m
因为如果 a - b 是 m 的倍数,则 a - b ≡ 0 (mod m),也就意味着下式是成立的。
a ≡ b (mod m)
又因为
(a - b) × C ≡ J × m
所以 (a - b) × C 是 m 的倍数。如果 C 和 m 互质,则 a - b 含有 m 所有的质因数。
换言之,a - b 是 m 的倍数,所以可以写成 a - b = K × m 这种形式。
嗯,在这里“互质指的是没有共同的质因数”又派上用场了。
解答7-1 (同余式和除法运算)
假设a, b, C, m 为整数。
当 C 与 m 互质时,以下式子成立。