9.4 自己家
9.4 自己家
晚上。
我在自己的房间里看着村木老师给我的卡片。我设定的问题是这样子的。
问题 9-2
若下面的无穷级数收敛,求它的值。若不收敛,请证明。
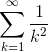
首先,把 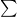 具体地写出来,捕捉式子的感觉。
具体地写出来,捕捉式子的感觉。
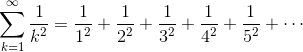
逐项看了看,但是好像不是很简单就能抓住线索的。试试数值计算吧?也就是说,先不管 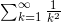 这个无穷级数,而是用具体的 n 来计算
这个无穷级数,而是用具体的 n 来计算 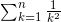 的部分和。白天只是一个劲地钻研泰朵拉的卡片了,数值计算也只进行了一点。
的部分和。白天只是一个劲地钻研泰朵拉的卡片了,数值计算也只进行了一点。
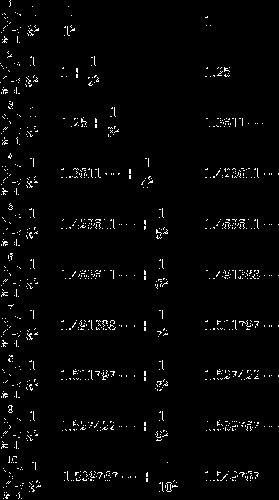
还不是很明白,画图像看看吧。
打开书包却没找到画图像用的纸。咦?难道忘在学校里了?
部分和好像不是急剧增加,但是也不能说是收敛的,就像前几天的那个调和级数那样缓缓地发散。
这么说来,这个式子与调和级数很相似。

不同的只有一点,k 的指数。这次的问题 9-2,因为是求 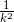 的和,所以 k 的指数是 2。另一方面,调和级数因为是求
的和,所以 k 的指数是 2。另一方面,调和级数因为是求 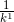 的和,所以 k 的指数是 1。
的和,所以 k 的指数是 1。
指数,指数。这么说起来,米尔嘉告诉过我什么是 ζ 函数。我把 ζ 函数的定义在笔记本上又写了下来。
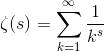 (ζ 函数的定义式)
(ζ 函数的定义式)
使用这个定义,调和级数就可以表示成 ζ(1)。
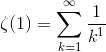 (用 ζ 函数来表示调和级数)
(用 ζ 函数来表示调和级数)
问题 9-2 也可以写成 ? 函数的形式。因为指数是 2,所以就是 ζ(2)。
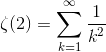 (用 ζ 函数来表示问题 9-2)
(用 ζ 函数来表示问题 9-2)
名字,名字。但是,虽然这样命名了,可思路并没有打开啊。