从我们的术语到标准术语
同类相食微积分
课本上称为“变分法”,在第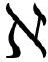 章介绍的。它指的是将微积分工具应用于课本上所说的“泛函”(参见词条“同类相食机器”)。
章介绍的。它指的是将微积分工具应用于课本上所说的“泛函”(参见词条“同类相食机器”)。
同类相食机器
课本上称为“泛函”,在第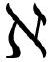 章介绍的。它指的是吞食整台机器吐出来一个数的“大机器”,不同于f(x)≡x2这类较简单的吞食一个数吐出来一个数的机器。例如,下面是三个同类相食机器的例子:
章介绍的。它指的是吞食整台机器吐出来一个数的“大机器”,不同于f(x)≡x2这类较简单的吞食一个数吐出来一个数的机器。例如,下面是三个同类相食机器的例子:
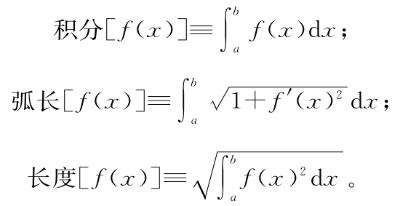
第一个例子是吞食机器f(x)吐出来它在x=a和x=b之间的图形下的面积的同类相食机器。第二个例子是吞食机器f(x)吐出来它在x=a和x=b之间的图形的长度的同类相食机器。第三个是吞食机器f(x),将机器视为无穷多格子组成的向量(即无穷维空间中的一个点),吐出来向量“长度”的同类相食机器。第三个例子的“长度”不是f的图形的长度,而是将捷径公式推广用于无穷维(更详细的讨论参见第N章)。
捷径公式
课本上称为“勾股定理”(对这个公式为何成立的一个简单图形解释,参见开始的插曲1)。这个公式也是课本上所说的“三角恒等式”的来源。例如,由于正弦和余弦就是指长度为1的斜线的垂直和水平长度(参见词条V和H),因此捷径公式告诉我们
(垂直长度)2+(水平长度)2=(总长度)2。
这可以简写为
sin2(x)+cos2(x)=1。
课本上会给源自上面等式的其他“三角恒等式”起多余的名字。例如,如果将上面等式的两边除以cos2(x),可以得到
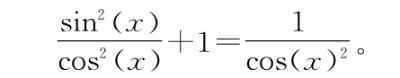
教科书会用tan(x)表示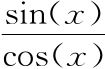 ,用sec(x)表示
,用sec(x)表示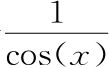 ,这就会变成
,这就会变成
tan2(x)+1=sec2(x)。
因此这个所谓的“三角恒等式”其实就是捷径公式,其实就是把V和H的简单组合用各种晦涩的名称隐藏起来。
H
课本上称为“余弦”。我们用这个词表示“水平(Horizontal)”。相对于水平轴倾斜角度为α的单位长度直线的水平长度为cos(α),我们称之为H(α)。参见V,即课本上说的“正弦”。
倒立
课本上称为“倒数”。例如,3的倒立是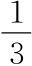 。我们不经常使用这个词。不过数学家也不经常用“倒数”。也许两者都可以不要。
。我们不经常使用这个词。不过数学家也不经常用“倒数”。也许两者都可以不要。
无穷放大镜
这个词在标准课本中没有直接的对应,虽然它与局部线性和极限的概念有关。无穷放大镜是一个假想的工具,我们可以用它来无穷放大任何东西。它被用来推动微积分的核心思想:将弯曲的东西无穷放大,看起来就会像是直的。通过想象这个无穷放大的过程,我们可以将涉及弯曲东西的问题化简为涉及微小的直东西的问题,从而可以用更简单的方法解决。详细讨论见第2章。
机器
课本上称为“函数”。在整本书中都有使用。
撕东西显然律
出于好玩取的名字,不常用。课本上称为“分配律”。它将加和乘关联到一起,说的是对于任何数a、b和c,以下式子成立:
a(b+c)=ab+ac,
(b+c)a=ba+ca。
由于乘的顺序无关紧要,因此有ab=ba和ac=ca,因此当a和b都是数时上面的两行是等同的(不过如果a和b表示更抽象的对象,它们可能不等同,后面会简要解释)。我们之所以称之为撕东西显然律,是因为如果将a(b+c)视为长为a宽为b+c的矩形的面积,分配律就可以解释为如果将矩形撕成两半,面积不变。这个术语主要在第1章用。
虽然我们在书中没有深入讨论抽象代数,我们还是可以在更广义的背景下定义“分配律”。一般来说,分配律是一个将两个二元操作以某种方式结合到一起的命题。什么是二元操作?是这样,给定两个对象[1]a和b,二元操作是将两个对象绑定到一起得到第三个对象a★b的一种抽象方式。在抽象代数中,如果以下两条语句对所有对象a、b和c都成立,我们就说二元操作★对另一个二元操作◇可“分配”:
a★(b◇c)=(a★b)◇(a★c),
(b◇c)★a=(b★a)◇(c★a)。
注意其与前面更熟悉的针对数的版本的相似性。在历史上,针对数的版本被先发现,然后才推广到更广义和更怪异的条件。
怀旧装置
课本上称为“泰勒级数”和“麦克劳林级数”。
加乘机器
课本上称为“多项式”。我们取这个名字是因为它们是可以只用加和乘就能描述的机器。加乘机器定义为具有如下形式的任何机器
m(x)≡#0+#1x+#2x2+…+#nxn,
其中符号#i表示固定的数。
捷径
课本上称为“弦”。参见“捷径公式”。
T
课本上称为“正切(Tangent)”,在插曲6“干掉#”有用到。教科书用缩写tan(x)表示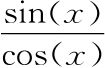 ,也就是我们说的
,也就是我们说的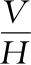 。参见词条V和H,也即课本上的“正弦”和“余弦”。
。参见词条V和H,也即课本上的“正弦”和“余弦”。
V
课本上称为“正弦”。我们用这个名字表示“垂直(Vertical)”。这样用是因为角度为α的倾斜直线垂直长度为sin(α),也就是我们说的V(α)。参见词条H,也即课本上的“余弦”。
Λ
课本上称为“反正弦”,记为arcsin(x)或sin-1(x),在插曲6“干掉#”有用到。我们用这个名称是因为希腊字母Λ看起来像倒过来的V,而我们用V表示课本上说的“正弦”(参见词条V)。对所有x,机器Λ的定义满足
V(Λ(x))=x 和 Λ(V(x))=x。
不过这台机器不是对所有x都有无歧义的定义,因为V重复自身(用数学行话来说,不是“一一对应”)。例如,用标准符号π表示我们在书中说的#,对所有正整数和负整数n,都有V(nπ)=0。因此,与Λ(0)对应的数不是唯一的,因为任何nπ(例如-2π、-π、0、π、2π,等等)都是同等合法的选择。一个常见的传统是将Λ(x)不是定义为V(x)的反函数,而是局限于一个小的实数子集的V(x)的“反函数”或“相反机器”。例如,如果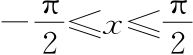 ,则机器V(x)不会重复自身;不同输入会得到不同输出。也就是说,对于
,则机器V(x)不会重复自身;不同输入会得到不同输出。也就是说,对于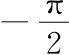 和
和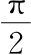 之间的所有数x和y,如果x≠y,则V(x)≠V(y)。因此,Λ通常定义为机器V的这个受限版本的“反函数”或“相反机器”。不过这是相当无趣的技术细节。我们发现除了极少数情形,在这本书的大多数背景下没有必要讨论“反函数”。
之间的所有数x和y,如果x≠y,则V(x)≠V(y)。因此,Λ通常定义为机器V的这个受限版本的“反函数”或“相反机器”。不过这是相当无趣的技术细节。我们发现除了极少数情形,在这本书的大多数背景下没有必要讨论“反函数”。
⊥
在插曲6“干掉#”中有用到,课本上称为“反正切”,通常记为arctan(x)或tan-1(x)。我们取这个名字是因为符号⊥看起来像倒过来的T,而我们是用T表示课本上说的“正切”(参见词条T)。机器⊥定义为满足
T(⊥(x))=x 和 ⊥(T(x))=x。
#
课本上称为π。第4章第1节有它的定义,以及为什么我们不采用标准标记的讨论。简而言之:我们称之为#是提醒我们自己它是一个我们根据其性质定义的数,并且在我们知道其具体数值之前就能从概念上利用它(在插曲6“干掉#”中我们最终算出了它的具体数值)。因为大部分读者都很熟悉符号π,称这个概念为π会让我们容易忘记——在我们旅程的大多数时候——我们其实并不“知道”这个数约等于3.14。
[1] 这些“对象”可以是数,也可以是其他东西,例如矩阵(书中没有深入讨论)或函数。