N.2.3 坐标轴:(不,能)(没,有)(它,们)
我们首先尝试发明一些缩写,将式(N.10)表述为更简单的形式。我们先用v作为机器的输出的缩写,因此
v≡(x1,x2,…,xn)
是所有n个变量组成的列表。课本上用“向量”表示它们,也就是v。“向量”这个词听起来可能有点怪异和老旧,但说起来也有点意思,我们就把它留着。我们用粗体写向量v以提醒我们它与数是不同类型的东西。我们用dvi作为除了第i格其他格都为0的向量,第i格为无穷小量dxi。即:
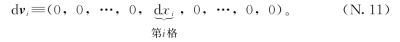
有了这些约定,我们可以把式(N.10)的杂乱定义写成这样:
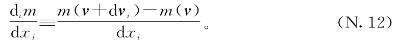
这样好看了一点,当然也更节省空间,但是出于一个全新的理由,这个标记还是让人迷惑。为什么?嗯,上面这个等式一眼看过去让人感觉在新的多变量世界中的导数与单变量世界的导数似乎不一样。哪里不一样?在上面的等式中,上面的dvi是一个“微小向量”,而底下的dxi又是一个“微小的数”。也就是说,在这个等式中似乎有两种不同类型的微小的东西:微小的数和微小的向量。但这其实是因为我们选择新的缩写让等式(N.10)看起来不那么疯狂的缘故。
等式(N.10)虽然有缺陷,但还是清晰多了,因为上面和下面其实是同一种微小的东西。这反而澄清了这个导数具有它一贯具有的相同解释。即我们可以这样谈论导数:
1.我们从机器m开始,喂给它某个东西s,它会吐出来m(s)。
2.我们将喂给机器的东西做微小的改变,从s变成s+ds。这会使得输出从m(s)变成m(s+ds)。
3.我们将输出的变化缩写为dm≡m(s+ds)-m(s)。如果我们有多个变量,可能需要改变我们的缩写以提醒自己改变的是什么。
4.无论喂进去的s是一个数、向量,还是整台机器,导数的概念都是一样的。m的导数定义为输出dm的微小改变除以输入ds的微小改变。
因此等式(N.10)和等式(N.12)这两个缩写各有利弊。我们面临着怪异的第22条军规。我们很快会看到,第22条军规远不限于这个例子。