N.2.1 简单的概括和难解的缩写
在上面的对话中，我们“发明”了多变量微积分。我们研究了吞进去一个数吐出来两个数的机器，例如m（x）≡（f（x），g（x））。课本上称这些为“向量值函数”，意思是它们吞进去一个数吐出来的是向量。“向量”的意思同（我们说的）“列表”基本是一回事，在这本书后面的部分，我会交叉使用这两个术语。请注意我们这里的前数学论证对n个格子的向量同样成立。也就是说，我们可以要求n个格子的列表有如下性质：
（x1，x2，…，xn）+（y1，y2，…，yn）=（x1+y1，x2+y2，…，xn+yn）
c·（x1，x2，…，xn）=（cx1，cx2，…，cxn）。
同样，我们可以做能想到的最简单的事情。我们可以通过这些定义，以上面对话中一样的方式，证明“一进n出”的机器
m（x）≡（f1（x），f2（x），…，fn（x））
的导数是我们所能期望的最简单的东西，即
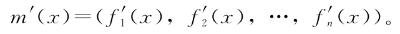
类似的，对于吞进去两个数吐出来一个数的机器，可以缩写为m（x，y），我们也找到了与单变量微积分类似的处理方法。我们直接定义了两个不同的导数：每个输入一个。也就是说，我们有相对于x的导数（将y视为常量），和相对于y的导数（将x视为常量）。我们决定将这些表述为：
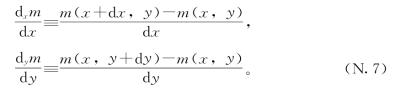
课本上称这些为“偏导数”。它们把左边的称为“m相对于x的偏导数”，把右边的称为“m相对于y的偏导数”。但这些偏导数并不“偏”：它们的计算与第2章的导数的计算是一样的。注意我们可以在不改变y的条件下改变x（反过来也是一样），因此我们可以写出这些式子：
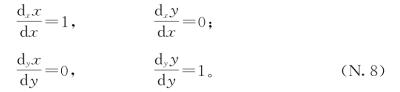
同样，m（x，y）的格子数量为两个也没有什么特殊的。我们可以对有n个格子的机器做类似的定义和论证。如果将m定义为吞进去n个数吐出来一个数的机器，写作
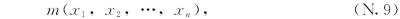
我们就有n个格子，因此有n个不同的导数：一个对应x1，一个对应x2，依此类推，直到xn。同前面一样，我们可以这样定义导数：
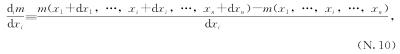
其中我们记为di而不是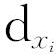
，因为后者有下标的下标，有点复杂。虽然上面的等式难看得足以让你血压升高，它所表达的内容却极其简单：“n进一出”机器相对于某个变量xi的导数。就是前面一样的东西。我们只需无视不是xi的一切，然后将xi视为唯一的变量做单变量微积分。看得出来这其实没有新东西了吗？下一节我们就会用更简洁的缩写来表示上面这个标记。