6.2 基本锤子的实际测试

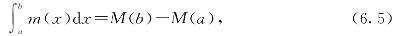
我们知道如何求矩形的面积，所以我们用常数机器m（x）≡＃的图形来检验一下这个思想。这台机器就是高度为＃的水平线，它在x=a和x=b两点间的图形就是高为＃宽为b-a的矩形，因此面积应当是＃·（b-a）。现在，如果我们关于反导数的思想是正确的，就应该有

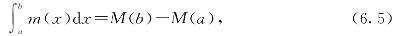
其中m（x）≡＃，M（x）则是m（x）的“反导数”。也就是说，M（x）是导数为m（x）的任意机器，即M'（x）=m（x）=＃。我们还不知道怎么求反导数，因此只能利用我们熟悉的导数，再加上一点乐观精神，盯着机器m（x）≡＃看，直到想起它是谁的导数。幸运地是，在这个例子中，这并不难，因为我们知道（＃x）'=＃。这告诉我们M（x）=＃x，我们可以用它来检验一下我们的思想能不能给出正确答案。

在x=a和x=b两点之间，水平直线m（x）≡＃图形下面的面积必定是＃·（b-a），因为它就是一个矩形。因此在这个特例中，我们奇怪的新符号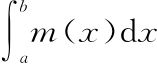应该等于＃·（b-a）。我们还不确信这个新符号是否真是反导数的差，但现在可以检验了！由于我们发现M（x）=＃x，因此M（b）-M（a）=＃b-＃a，而这正好就是＃·（b-a）。

太好了！我们用两种方法得出了同样的答案。注意我们没有利用等式（6.5）。这很好。我们还不想假定它成立。我们只是用不同方法计算两边，然后证明在这个简单情形中等式（6.5）成立。我们继续。