放大镜回归
作者：好吧，假设我们得到了某台机器M。
读者：是的。
数学：什么机器？
读者：最好不要限定。我们可以先设它为未知。
作者：是的，这样我们就得到了某台绘制出来为弯曲的机器。斯蒂夫建议我们照以前的方法处理。
读者：也就是选个点然后无穷放大。
数学：然后呢？
读者：是这样，一旦我们放大，它就像是直的。这样我们也许就可以假装在那一点处弯曲东西下面的微小面积为矩形。
数学：能够画出来吗？这样我才能跟上思路。
作者：可以。
（读者画了图5.3。）
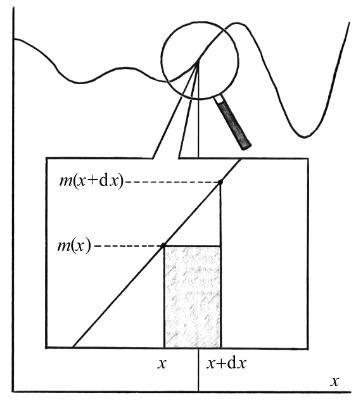
图5.3 尝试用无穷放大镜来计算弯曲的东西下面的面积。我们目前的设想是这样。第1步：画出弯曲的东西。第2步：选一个位置放大。第3步：看能不能将弯曲东西那一点下面的面积写为无限薄的矩形。如果能做到，每个薄矩形的面积就是“长乘以宽”或m（x）dx。然后我们就能对每一点x，将所有这些微小的面积加到一起。因此如果我们知道怎么把无穷多个无穷小量加总，也许我们就能做到！
作者：等一下。在你画的图里，少了一些面积。看到那个空白三角形了吗？我认为得把它填上，否则我们就得不到正确答案。
数学：那倒不一定有问题！……
［数学开始了一段（（相当）冗长的）（可有可无的（！））（半）题外话。］
数学：你们看，这些无穷小量似乎是分层次的，至少看上去是这样。也就是说，3和99这样的数在某种意义上说比7dx或52ds这样的数“高一层”，比6dxdy或99dsdt这样的数高两层。当不同层的多个项相加时，在某种意义上似乎只有最高层才重要。例如3与3+2dx无穷接近，因此当我们问3+2dx多大时，我们的答案不会远离3。但在另一种意义上，在开始问这个数的大小之前，低层也重要。低层不能忽视，因为有时候，我们进行的运算可能会将高层的项相互抵消。在你们对导数的定义中就可以看到这一点。我用“拉扯X”作为“减去X的最高层的数，将结果除以dx”的缩写。现在如果我们问9+6dx+（dx）2多大，答案就是9。当然，9这个数也会告诉我们同样的事情。因此似乎一开始就可以将低层的数忽略掉。其实不能忽略。一旦拉扯它们，9和9+6dx+（dx）2就会有不同的表现。拉扯9+6dx+（dx）2会得到6+dx，这个数的大小是6。而拉扯9会变成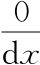
，这就是0。因此对无穷小量，低层不能忽略，但一旦我们开始问这个数有多大，就只需要关注最高层的数了。
［数学的（半）题外话结束。］
斯蒂芬·克莱尼：我不确定自己对此有何看法。
读者：我也是。
作者：这与忽略空白三角形有何关系？
数学：哦，是的，回到图5.3。点x下面的瘦高矩形的面积为m（x）dx。缺失的三角形面积为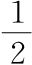
dxdM，这个要低一层。因此我们可以忽略它，因为我们只是把面积相加，而不是拉扯它们。
读者：这有点吓到我了。
作者：是的，我也不明白你的意思。
斯蒂芬·克莱尼：为什么你老是说“拉扯”？
数学：抱歉……
作者：我认为我们可以只考虑常规矩形，不是无穷小的那些，然后想象将它们越缩越小。
数学：怎么做？
作者：就像这样：
（作者画了图5.4，然后在图题中说明了一切。）
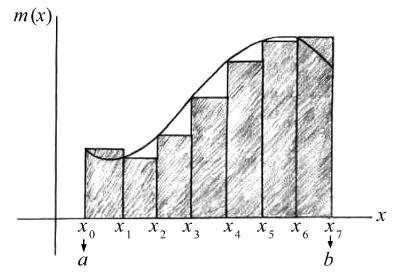
图5.4 作者：噢，比我预想的要挤一些。是这样，我们想求出点x=a和x=b之间弯曲的东西下面的面积。如果觉得无限多个薄矩形太古怪了，我们可以想象用有限个矩形。就像图中画的那样。想象在x=a和x=b之间选一堆点。给这些点命名为x1，x2，…，xn，这样就可以方便地重新缩写为a≡x0和b≡xn+1。对每个点xi，机器的图形的高度就是矩形的高度。这样高度就有了。每个矩形的宽度则是点与下一个点之间的距离，如图所示。每个矩形有一个小的宽度Δxi≡xi+1-xi。因此每个矩形的面积就是“高乘以宽”，即m（xi）Δxi。如果我们将所有矩形的面积相加，不会得到刚好正确的面积，但应该很接近。如果我们想象增加越来越多的矩形，让每个矩形变得越来越薄，我们就越来越接近正确的面积。因此不难。我的意思是，不难想象。真这样去做可能有点痛苦。因此最好还是别去做……喔，这个图题有点长。不知道他们还在不在听。
数学：我们还在听。[1]
（作者从图题回来了，
数学从脚注回来了，
读者似乎是同时从图题和脚注回来了，
旁白查看了他的脚本，确保所有人都回来了……
……
唉，斯蒂夫和服务生不知去了
……哪里。）
数学：（对作者说）我想我明白了你的意思，图题中给出的答案基本是对的。我想我们也可以用这种方式思考。
读者：我不知道我理解得对不对，你是说弯曲的东西下面的面积几乎……但不完全……就是这个？……
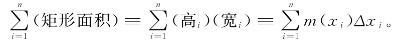
作者：喔，这比我说的简洁多了。不过，是的，就是这么回事。我就是这个意思
读者：为什么我们要用矩形做这个呢？根据图题？
作者：噢，不用。至少我不想。我的意思是，无限多个矩形的思想很棒。但我们不知道如何实际应用，去算出某个东西。因此图题中的思想并不是说我认为要实际去做。但至少可以让我们计算具体的数。假想的计算。如果我们想算的话就可以算。而且随着我们增加更多矩形，我们就会逐渐接近数学所说的那个正确答案。
数学：我更喜欢我的思路。
作者：我也是。我已经想放弃这个问题了。
数学：我也是。
读者：好吧。那我们就放弃吧！我们能再次用莫里哀手法吗？
作者：当然！我们以前决定放弃的时候都是这么干的。虽然我们还不知道如何计算确切的答案，给它命个名不会碍事。不过取的名字最好能提醒我们它是什么。
读者：是的，我们可以这样来表示这个近似答案：
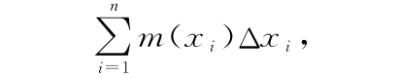
所以我们就用这个来给确切答案构建一个缩写。你之前提到课本上用Δ某个东西作为“某个东西中两点之间的差异”的简写，因为Δ就是希腊字母中的d，而d表示差异（Difference），或者距离（Distance）。我觉得我们还没有决定。
作者：我也觉得。
读者：管他呢，既然这样，在我们发明微积分的时候，我们需要用另一种方式谈论差异，只是这次是无穷小。因此我们就把希腊字母Δ替换为拉丁字母d。这样dx或dt或d（某个东西）就都表示无限接近的两个点之间某个量的差异。这样新的思想就有点像原来的思想。
数学：这对我们有什么用呢？
读者：我们放弃了，记得吗？因此我们要用莫里哀手法给我们求不出的这个东西取一个名字。
数学：哦，是的。我忘了。那我们给它取什么名字呢？
读者：是这样，我刚才已经在上面写了近似答案。作者在图题中对此进行了描述。因此我们可以用那个缩写，将Δ换成d，因为我们的矩形是无限薄的。这样我们就得到
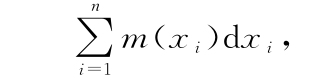
但我想这并没有意味着什么，因为我们一次只改变了一个缩写。
作者：是的！确切的答案应当有无穷多个矩形，每个x点对应一个，因此xi标记就不再适用了——i是对矩形计数，但如果线上每个点都对应一个矩形，我们就无法计数了。因此不能再用i。i=1到n也没法用了。它们只不过是告诉我们开始和结束的地方，但是现在我们又可以重新称它们为a和b。因此我想现在我们可以这样缩写
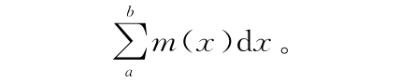
我们可以就停在这里然后——
数学：好了！我在等你说完。现在轮到我来改了。
作者：喔，已经没有什么可以改的了。我们基本已经做完——
数学：作者，我们是三个人。读者将希腊字母Δ改成了拉丁字母d。你把下标去掉了。要让我也改点什么才公平。公平性关系到不变性。你喜欢不变性吗？
作者：（不情愿地）……喜欢。
数学：那就好！我顺着读者的思路走。∑是希腊字母的S，表示“求和（Sum）”。同以前一样，要将我们的缩写从有限转换成无限，可以将希腊字母换成相应的拉丁字母，就像这样：
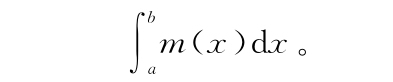
读者：那是什么？！
作者：啊……嗯……数学？那不是S。
数学：用笔对于你们手指灵活的灵长类来说很容易，但我不是物理存在。
作者：理解。只是看起来有点好笑。不过就这样吧。
数学：那这到底代表什么呢？
读者：嗯，我们命名时很小心，应该能搞清楚。这个S形的东西提醒我们它是求和，是用拉丁字母代替了希腊字母，m（x）是高，dx是无穷小的宽。因此它表示的是对无穷多个东西求和，其中每一个都是一个无穷薄矩形的面积。而a和b则是提醒我们开始和结束的地方。
作者：棒极了！我们成功运用了莫里哀手法！
读者：也就是我们成功地……什么也没做？
作者：好吧，是的。不过我们可以将这个东西写成这样了：
（x=a和x=b之间m的图形下面的面积）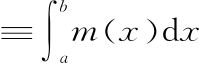
，
但你是对的。我们还是不知道怎么计算它，我们并没有真的“做”什么。
读者：因此我们还是没有离解决问题更近？
斯蒂芬·克莱尼：正是！
（大家看着斯蒂夫。）
作者：（对斯蒂夫说）你不会是一直在这里听我们说吧？
斯蒂芬·克莱尼：没有，只是这似乎是一个很好的时机说“正是”。我回了数学的房子。元——
作者：我还以为你和服务生在一起呢。
斯蒂芬·克莱尼：没有。那是你写的我在那里。
作者：啊？我不记得我写——
斯蒂芬·克莱尼：管他呢，我告诉你们吧，元需要帮助，所以我就回去了。
数学：帮助什么？
斯蒂芬·克莱尼：我正要说这个。
（斯蒂夫从外套里拿出一个小装置，对着它讲话。）
斯蒂芬·克莱尼：元？……好吧。我们就来。
[1] 读者：什么？数学：哦，我想这可能有点乱。去读一下图5.4下面的文字吧。我在这里等你。