5.2 四种机器

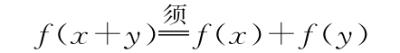
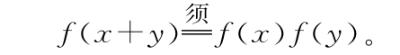
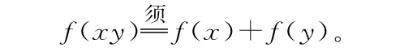
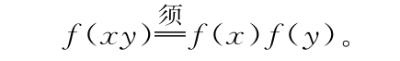
虚空中包含了无穷多种等待被发明的东西，但其中多数都很乏味无趣。维特根斯坦（Ludwig Wittgenstein）说：“对于不可言说的，必须保持沉默。”这句话对数学同样成立。这些思想提醒我们，根据性质来定义数学对象是避开虚空中乏味无趣部分的稳妥方式。如果我们以对象的性质来定义对象，我们就总是可以知道它能说什么，即便我们也许不知道它“是”什么。在这一节我们将看到几个体现了这一原则的特别惊人的例子。考虑到加和乘到目前为止在我们的旅程中扮演的核心角色，让我们根据机器在面对这两种操作时的性质来定义四种机器。就目前来说，把玩这些机器纯粹是出于美学动机。

四种机器

AA型机器定义为所有将加（Add）转换为加（Add）的机器：

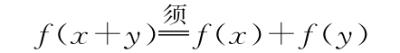
AM型机器定义为所有将加（Add）转换为乘（Multiply）的机器：

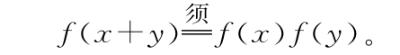
MA型机器定义为所有将乘（Multiply）转换为加（Add）的机器：

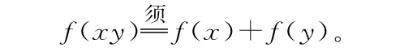
MM型机器定义为所有将乘（Multiply）转换为乘（Multiply）的机器：

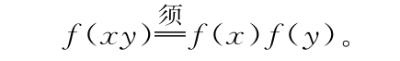
在这四种机器的定义中，我们要求每个语句对所有数字x和y都成立。这是四种特别优雅的性质，但现在我们还不知道这些机器类型的成员长什么样。也许一些类型没有成员。写出不可能为真的语句是完全有可能的，虽然这种不可能不那么容易一下就看出来。我们先来熟悉一下这些机器类型，看能不能搞清楚它们的样子。